3.3. Free Streaming

The most salient feature of hot DM is the erasure of small fluctuations by free streaming. Thus even collisionless particles effectively exhibit a Jeans mass. It is easy to see that the minimum mass of a surviving fluctuation is of order M³_Pl / m² [42, 43]. Let us suppose that some process in the very early universe - for example, thermal fluctuations subsequently vastly inflated in the inflationary scenario - gave rise to adiabatic fluctuations on all scales. In adiabatic fluctuations, all the components - radiation and matter - fluctuate together. Neutrinos of nonzero mass m stream relativistically from decoupling until the temperature drops to T ~ m, during which time they traverse a distance d = R_H(T = m) ~ M_Pl, m^-2. In order to survive this free streaming, a neutrino fluctuation must be larger in linear dimension than d. Correspondingly, the minimum mass in neutrinos of a surviving fluctuation is M_J, ~ d³ m n(T = m) ~ d³ m⁴ ~ M³_Pl m^-2. By analogy with Jeans's calculation of the minimum mass of an ordinary fluid perturbation for which gravity can overcome pressure, this is referred to as the (free-streaming) Jeans mass.

A more careful calculation [43, [44] gives

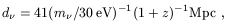
(7)

that is, d = 41 (m / 30 eV)^-1 Mpc in comoving coordinates, and correspondingly

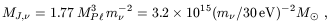
(8)

which is the mass scale of superclusters. Objects of this size are the first to form in a -dominated universe, and smaller scale structures such as galaxies can form only after the initial collapse of supercluster-size fluctuations.

When a fluctuation of total mass ~ 10¹⁵ M enters the horizon at z ~ 10⁴, the density contrast _RB of the radiation plus baryons ceases growing and instead starts oscillating as an acoustic wave, while that of the massive neutrinos continues to grow linearly with the scale factor R = (1 + z)^-1 since the Compton drag that prevents growth of _RB does not affect the neutrinos. By recombination, at z_r ~ 10³, _RB / 10^-1, with possible additional suppression of _RB by Silk damping. Thus the hot DM scheme with adiabatic primordial fluctuations predicts small-angle fluctuations in the microwave background radiation that are lower than in the adiabatic baryonic cosmology, which was one of the reasons HDM appealed to Zel'dovich and other theorists. Similar considerations apply in the warm and cold DM schemes. However, as we will discuss in a moment, the HDM top-down sequence of cosmogony is wrong, and with the COBE normalization hardly any structure would form by the present.

In numerical simulations of dissipationless gravitational clustering starting with a fluctuation spectrum appropriately peaked at ~ d (reflecting damping by free streaming below that size and less time for growth of the fluctuation amplitude above it), the regions of high density form a network of filaments, with the highest densities occurring at the intersections and with voids in between [45, 46, 47, 48]. The similarity of these features to those seen in observations was cited as evidence in favor of HDM [49].