5. EVIDENCE FOR NEUTRINO MASS FROM OSCILLATIONS

There is mounting astrophysical and laboratory data suggesting that neutrinos oscillate from one species to another [27], which can only happen if they have non-zero mass. Of these experimental results, the ones that are regarded as probably most secure are those concerning atmospheric neutrino oscillations from Super-Kamiokande (see the chapter by John Learned) and solar neutrinos from several experiments (see the chapter by Wick Haxton). But the experimental results that are most relevant to neutrinos as hot dark matter are from the Liquid Scintillator Neutrino Detector (LSND) experiment at Los Alamos (see the chapter by David Caldwell).

Older Kamiokande data [83] showed that, for events attributable to atmospheric neutrinos with visible energy E > 1.3 GeV, the deficit of _µ increases with zenith angle. The Super-Kamiokande detector has confirmed and extended the results of its smaller predecessor [84]. These data imply that _µ -> oscillations occur with a large mixing angle sin² 2 > 0.82 and an oscillation length several times the height of the atmosphere, which implies that 5 x 10^-4 < m² _µ < 6 x 10^-3 eV² (90% CL). (Neutrino oscillation experiments measure not the masses, but rather the difference of the squared masses, of the oscillating species, here m _µ² |m()² - m(_µ)²|.) This in turn implies that if other data requires either _µ or to have large enough mass ( 1 eV) to be a hot dark matter particle, then they must be nearly equal in mass, i.e., the hot dark matter mass would be shared between these two neutrino species. Both the new Super-Kamiokande atmospheric _e data and the lack of a deficit of _e in the CHOOZ reactor experiment [85] make it quite unlikely that the atmospheric neutrino oscillation is _µ -> _e. If the oscillation were instead to a sterile neutrino, the large mixing angle implies that this sterile species would become populated in the early universe and lead to too much ⁴He production during the Big Bang Nucleosynthesis epoch [86]. (Sterile neutrinos are discussed further below.) It may be possible to verify that _µ -> oscillations occur via a long-baseline neutrino oscillation experiment. The K2K experiment is looking for missing _µ due to _µ -> oscillations with a beam of _µ from the Japanese KEK accelerator directed at the Super-Kamiokande detector, with more powerful Fermilab-Soudan and CERN-Gran Sasso long-baseline experiments in preparation, the latter of which will look for appearance.

The observation by LSND of events that appear to represent _µ -> _e oscillations followed by _e + p -> n + e⁺, n + p -> D + , with coincident detection of e⁺ and the 2.2 MeV neutron-capture -ray, suggests that m_{µ e}² > 0 [87]. The independent LSND data [88] suggesting that _µ -> _e oscillations are also occurring is consistent with, but has less statistical weight than, the LSND signal for _µ -> _e oscillations. Comparison of the latter with exclusion plots from other experiments allows two discrete values of m²_{µ e}, around 10.5 and 5.5 eV², or a range 2 eV² m²_{µ e} 0.2 eV². The lower limit in turn implies a lower limit m 0.5 eV, or 0.01 (0.65 / h)². This would imply that the contribution of hot dark matter to the cosmological density is at least as great as that of all the visible stars _* 0.0045 (0.65 / h) [89]. Such an important conclusion requires independent confirmation. The KArlsruhe Rutherford Medium Energy Neutrino (KARMEN) experiment has added shielding to decrease its background so that it can probe a similar region of m²_{µ e} and neutrino mixing angle; the KARMEN results exclude a significant portion of the LSND parameter space, and the numbers quoted above take into account the current KARMEN limits. The Booster Neutrino Experiment (BOONE) at Fermilab should attain greater sensitivity.

The observed deficit of solar electron neutrinos in three different types of experiments suggests that some of the _e undergo Mikheyev-Smirnov-Wolfenstein matter-enhanced oscillations _e -> _x to another species of neutrino _x with m_{e x}² 10^-5 eV² as they travel through the sun [90], or possibly ``Just-So'' vacuum oscillations with even smaller m<sub>e x</sub><sup>2</sup> [91]. The LSND <sub>µ</sub> -> <sub>e</sub> signal with a much larger m<sub>e µ</sub><sup>2</sup> is inconsistent with x = µ, and the Super-Kamiokande atmospheric neutrino oscillation data is inconsistent with x = . Thus a fourth neutrino species <sub>s</sub> is required if all these neutrino oscillations are actually occurring. Since the neutral weak boson Z<sup>0</sup> decays only to three species of neutrinos, any additional neutrino species <sub>s</sub> could not couple to the Z<sup>0</sup>, and is called ``sterile.'' This is perhaps distasteful, although many modern theories of particle physics beyond the standard model include the possibility of such sterile neutrinos. The resulting pattern of neutrino masses would have _e and _s very light, and m(_µ) m() (m_{e µ}²)^1/2, with the _µ and playing the role of the hot dark matter particles if their masses are high enough [92]. This neutrino spectrum might also explain how heavy elements are synthesized in core-collapse supernova explosions [93]. Note that the required solar neutrino mixing angle is very small, unlike that required to explain the atmospheric _µ deficit, so a sterile neutrino species would not be populated in the early universe and would not lead to too much ⁴He production.

Of course, if one or more of the indications of neutrino oscillations are wrong, then a sterile neutrino would not be needed and other patterns of neutrino masses are possible. But in any case the possibility remains of neutrinos having large enough mass to be hot dark matter. Assuming that the Super-Kamiokande data on atmospheric neutrinos are really telling us that _µ oscillates to , the two simplest possibilities regarding neutrino masses are as follows:

A) Neutrino masses are hierarchical like all the other fermion masses, increasing with generation, as in see-saw models. Then the Super-Kamiokande m² 0.003 implies m() 0.05 eV, corresponding to

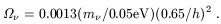
(11)

This is not big enough to affect galaxy formation significantly, but it is another puzzling cosmic coincidence that it is close to the contribution to the cosmic density from stars.

B) The strong mixing between the mu and tau neutrinos implied by the Super-Kamiokande data suggests that these neutrinos are also nearly equal in mass, as in the Zee model [94] and many modern models [91, 92] (although such strong mixing can also be explained in the context of hierarchical models based on the SO(10) Grand Unified Theory [95]). Then the above is just a lower limit. An upper limit is given by cosmological structure formation. In Cold + Hot Dark Matter (CHDM) models with _m = 1, we saw in the previous section that if is greater than about 0.2 the voids are too big and there is not enough early structure. In the next section we consider the upper limit on if _m 0.4, which is favored by a great deal of data.