Copyright © 1993 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
653-703 Copyright © 1993 by Annual Reviews. All rights reserved |
2.2 Analysis Procedures
The question of the best strategy in analyzing microwave background radiation observations is not fundamental but it is important because the data are exceedingly difficult to obtain and, as of this writing, no clear signal due to the microwave background radiation fluctuations has been reported. It is therefore reasonable to push statistical analysis to its limits in extracting information from these data, and parametric methods, which can be pushed much further than nonparemetric methods, are almost always used. Once fluctuations have been measured with good signal-to-noise ratio, questions of statistical procedures will largely disappear and work will focus on the actual distribution of fluctuations.
Considerable disagreement exists about the best techniques to use in statistical analyses of these types of data. There are two main points of view, ``frequentist'', and ``Bayesian'', described briefly below. We refer the reader to Readhead et al (1989) and references therein for more detailed discussions. Despite apparent similarities, and many common terms and definitions, there is a fundamental difference between these two points of view. Frequentist methods are absolute, in the sense that the probability of obtaining a certain set of data is evaluated by considering all datasets that might have been obtained, given our assumptions about the sky and knowledge of instrumental errors. Bayesian methods, on the other hand, are relative, in that the absolute probability of obtaining a certain set of data is of little interest. What matters is only the relative probability as the assumptions about the sky are varied. Frequentist methods tend to go awry with unlikely datasets, because the frequentist credo is good long-run performance, and what happens to unlikely datasets doesn't make much difference in the evaluation of long-run performance. Bayesian methods avoid this difficulty, because they do not consider long-run performance.
2.2.1
In observations of n fields we have the set
of observations {
When the fields are correlated the joint density function must include the
correlation matrix
(Kendall & Stuart 1977
vol 1).
From Bayes's
formula, the probability density of
where p(
2.2.2
Such tests are called powerful for obvious reasons, but
it is important to remember that maximizing the power does not
guarantee that the power is high. Likelihood ratio tests have low
power, in fact, on data where
2.2.3
Given the importance that we attach to observations of the microwave
background radiation, it seems wise to make use of all the available
statistical tools, and to base the interpretation of the observations
upon those aspects upon which different methods agree. Indeed,
disagreement amongst statistical methods is a sure sign of statistical
peculiarities in the data. Nevertheless statistical analyses can
easily obscure, rather than illuminate, the observations themselves.
For this reason we reproduce below, wherever possible, the actual
 T ±
T ±  by p(
by p( T,
T,  ), and the variance of the
distribution of microwave background radiation fluctuations on the
sky by
), and the variance of the
distribution of microwave background radiation fluctuations on the
sky by  T2mbr. For Gaussian fluctuations the
probability density is entirely determined by W(k) and we have
T2mbr. For Gaussian fluctuations the
probability density is entirely determined by W(k) and we have
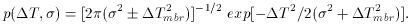
 Ti}, and the likelihood function,
L({
Ti}, and the likelihood function,
L({ Ti}|
Ti}| Tmbr), is defined by the joint
density function for the n fields. In the case that the n fields
are uncorrelated we have:
Tmbr), is defined by the joint
density function for the n fields. In the case that the n fields
are uncorrelated we have:
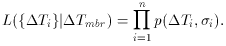
 Tmbr is
Tmbr is
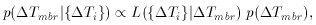
 Tmbr), called the prior probability
density, represents our knowledge of
Tmbr), called the prior probability
density, represents our knowledge of  Tmbr before the
observations. p(
Tmbr before the
observations. p( Tmbr|{
Tmbr|{ Ti}) is called the
posterior probability density. Since we have, in fact, no knowledge
of
Ti}) is called the
posterior probability density. Since we have, in fact, no knowledge
of  T we must assume a
prior probability density. The usual
practice is to make some such simple assumption as p(
T we must assume a
prior probability density. The usual
practice is to make some such simple assumption as p( Tmbr) = c
for
Tmbr) = c
for  Tmbr >>
0. Note that p(
Tmbr >>
0. Note that p( Tmbr) = 0 for
Tmbr) = 0 for  Tmbr < 0.
Tmbr < 0.
 Tmbr, we must
find
Tmbr, we must
find  Tmbr. The test is
simply a criterion by which we decide between an hypothesis H (e.g.,
that
Tmbr. The test is
simply a criterion by which we decide between an hypothesis H (e.g.,
that  Tmbr
Tmbr
 15 µK), and an
alternative hypothesis
K (e.g., that
15 µK), and an
alternative hypothesis
K (e.g., that  Tmbr > 15 µK). The level of
significance or size
Tmbr > 15 µK). The level of
significance or size  of the test is the
probability of rejecting H if H is true (a so-called Type I
error). The power of the test,
of the test is the
probability of rejecting H if H is true (a so-called Type I
error). The power of the test,  , is the probability of
rejecting H if K is true. Thus 1-
, is the probability of
rejecting H if K is true. Thus 1- is the probability of
accepting H when K is true (a so-called Type II error). Clearly
we would like a test for which
is the probability of
accepting H when K is true (a so-called Type II error). Clearly
we would like a test for which  is low, and
is low, and  is
high. It can be shown that a test based on the statistic S,
defined as the ratio of the likelihoods of the observations
is
high. It can be shown that a test based on the statistic S,
defined as the ratio of the likelihoods of the observations  Ti under H
and under K, maximizes the power
Ti under H
and under K, maximizes the power  for any given size
for any given size  of the test.
of the test.
 2 per degree of freedom,
2 per degree of freedom,
 2
2 , is much less than unity.
, is much less than unity.
 2
2 (reduced
(reduced  2) much less
than unity - which can happen if
measurement errors are overestimated or if the data are simply
atypical
(Readhead et al 1989).
In such cases the frequentist ``likelihood- ratio'' method can give
misleading results if the power of the test is low
(Lasenby 1981,
Cottingham 1987,
Lawrence et al 1988,
Readhead et al 1989).
For well-behaved datasets, with
2) much less
than unity - which can happen if
measurement errors are overestimated or if the data are simply
atypical
(Readhead et al 1989).
In such cases the frequentist ``likelihood- ratio'' method can give
misleading results if the power of the test is low
(Lasenby 1981,
Cottingham 1987,
Lawrence et al 1988,
Readhead et al 1989).
For well-behaved datasets, with
 2
2
 1, however, both frequentist and Bayesian methods
give comparable results. In our opinion, how a method is used
matters more than which one is used.
1, however, both frequentist and Bayesian methods
give comparable results. In our opinion, how a method is used
matters more than which one is used.
 T measurements with
their errors, since these convey, more
clearly than tables of 95% confidence limits, the real progress in
this field over the last decade.
T measurements with
their errors, since these convey, more
clearly than tables of 95% confidence limits, the real progress in
this field over the last decade.