Annu. Rev. Astron. Astrophys. 1992. 30: 653-703 Copyright © 1993 by Annual Reviews. All rights reserved

3.2 Observations on Angular Scales 1'-1°

Angular scales of 1'-1° are particularly important in theories of galaxy formation which assume the standard recombination model (Peebles & Yu 1970) in which the epoch of decoupling of the radiation from the matter occurs in the redshift range z ~ 1000-1500, and reionization occurs late, at z 10, when the universe is optically thin even if the intergalactic medium is completely ionized. Observations on these angular scales have all been filled aperture observations carried out on single dishes, although plans are afoot to construct interferometers which would operate at these resolutions (eg. Lasenby et al 1991). There have been four major efforts to detect anisotropy on these angular scales: by Uson and Wilkinson (1982, 1984a, b, c); by the group led by Readhead at the Owens Valley Radio Observatory of the California Institute of Technology (Readhead et al 1988, Lawrence et al 1988, Readhead et al 1989, Myers 1990, Myers et al 1991, Myers et al 1992); by the group led by Lubin at the University of California, Santa Barbara (Meinhold & Lubin 1991, Gaier et al 1992 in preparation); and by de Bernardis et al (1988, 1989, 1990). These four programs are discussed separately below.

3.2.1 ANISOTROPY OBSERVATIONS AT GREEN BANK, WEST VIRGINIA Uson and Wilkinson used the 140 foot antenna of the National Radio Astronomy Observatory at Green Bank, West Virginia at 19.5 GHz. The heterodyne reflected wave maser receiver (Moore & Clauss 1978, Moore 1980) had a bandwidth of 370 MHz and gave a system temperature in the range 50K-70K. The beam efficiency was 55% and the beamwidth (FWHM) was 1.5 arc minutes. The observations were made in five observing runs between December 1981 and March 1984. They used the nodding secondary mirror (at 3.33 Hz) to make double switching observations of at first 24 (first observing run) and later 12 (second-fifth observing runs) fields. The beamthrow was 4.5 arc minutes. The 140 foot telescope has an equatorial mount and the secondary mirror nods at a fixed angle relative to the hour circle of the field. The main field and the two reference fields are therefore all at different zenith angles. In order to minimize the effects of variable differential ground spillover Uson and Wilkinson observed fields as far north as practicable with the 140 foot telescope, at = 86° 51'.

Uson and Wilkinson used a double differencing scheme in which the beams were alternated on the fields of interest. They therefore measured the difference between a center field and the mean of two reference fields which straddled the center field at a distance of 4.5 arc minutes. This double differencing strategy is sensitive only to second and higher derivatives of the sky temperature as a function of position on the sky. It eliminates linear drifts and variations in the receiver, ground spillover, etc. With this strategy there remained a slow linear drift in the double-differenced output - i.e. a second order term - of about 55 mK per hour which is due to curvature in the scattered ground radiation. Each field was observed over the same range of zenith angles, and therefore this drift could be modelled. All of the published data have had this drift term subtracted out, i.e. both a mean term and a drift term have been subtracted. Uson and Wilkinson tracked their fields for either one hour (first observing run) or two hours (second-fifth observing runs). The culmination of this program led to firm upper limits on anisotropy well below T/T = 10^-4, (Uson & Wilkinson 1984a, b, c) and provided considerable impetus to the burgeoning amount of theoretical work in this area. Most important, these were the first results which appeared to rule out adiabatic fluctuations in baryonic matter as the primary agents of galaxy formation (e.g. Wilson & Silk 1981).

The results are shown in Figure 1a. The resulting upper limit on anisotropy calculated by Uson and Wilkinson is given in Table 3.

Table 3. 95% upper limits ^a on T/T at angular scales 1'-1°

Experiment	Angular Scale	T/T x 105	Comments
Uson & Wilkinson	1'.4	2.1	19.5 GHz; LR test, = 0.13
	1'.4	3.9	Bayesian (Readhead et al. 1989)
Readhead et al. 1989	1'.8	1.7	20 GHz; Bayesian, monochromatic W(k)
	1'.8	1.6	LR test, = 0.72; monochromatic W(k)
	12"	9.6	Bayesian; Gaussian W(k)
	2'.6	1.9	Bayesian; Gaussian W(k)
	25'	30	Bayesian; Gaussian W(k)
Myers et al. 1992	1'.8	4.5	20 GHz; Corrected for identified sources
			Bayesian; Gaussian W(k)
Berlin et al. 1984	4'.5-9'.5	1b	3.9 GHz; 1 , not 95%.
Meinhold & Lubin 1991	20'-30'	3.5	91 GHz; Gaussian W(k)
Alsop et al. 1992	30"	15	180 GHz, 270 GHz & 360 GHz; Gaussian W(k)
de Bernardis et al. 1990	15'-100'	20-30	270 GHz; Gaussian W(k)
a As described in the text, some of these observations detected excess variance which could not be definitively attributed to the cosmic microwave background radiation.
b Amirkhanyan (1987) calculates a limit of 30-50 x 10-5 (see text).

Uson and Wilkinson used a likelihood ratio test, to derive their limit on anisotropy. As we described in Section 2, likelihood ratio tests give misleading results when used on datasets with reduced ² values significantly less than unity. Unfortunately the Uson and Wilkinson data set has ² = 0.7. This can be seen directly in the data shown in Figure 1a, where it is clear that the measured values of T are closer to zero than would be expected based on the size of the error bars.

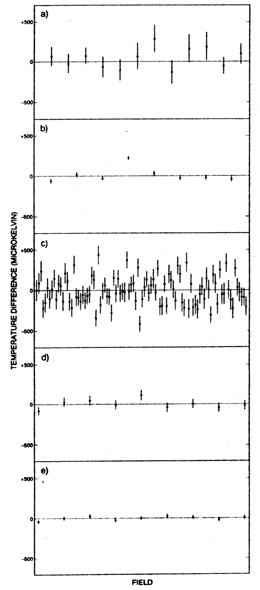
Figure 1. Observations of the microwave background radiation on angular scales 1'-1°. (a) Uson & Wilkinson (1984c) at 19.5 GHz, from twelve fields; (b) Readhead et al (1989) at 20 GHz - the eight observed fields in the OVRO ``NCP'' program; (c) Myers et al (1992) at 20 GHz - the 96 fields in the OVRO ``RING'' program, showing clear evidence of fluctuations which have been only partially identified with discrete sources (see text); (d) Meinhold & Lubin (1991) at 91 GHz - the ``South Pole'' results; (e) Gaier et al (1992 in preparation) - the 32.5-35 GHz channel from the December 1990-January 1991 observations. Double switching was used in (a), (b), and (c) and single switching in (d) and (e). No offsets or drifts have been subtracted in (b) and (c).

In the likelihood ratio test the observed variance in the means for each field is ascribed to the incoherent addition of the variance due to the noise in the observations (as given by the errors on each field) and the variance due to the sky noise (which we are trying to estimate). In the case of the present data set, given the relatively high values of the individual errors, the low scatter of the mean values about zero can only be accommodated in this test by ascribing a very low value to the sky variance. It is now understood that this pitfall can be detected in the likelihood ratio test by considering the power in addition to the size of the test (Readhead et al 1989, Bernstein et al 1989, Vittorio & Muciaccia 1991). In the Uson and Wilkinson data set the likelihood ratio test has a power of only 0.13, which is very low. Analysis of the data set using the Bayesian method yields a 95% confidence upper limit on anisotropy of T/T < 3.9 x 10^-5 (Readhead et al 1989).