2.2.2 The luminosity function of galaxies

A first attempt to find the luminosity function of extragalactic objects was made by Wirtz in 1926. His tabulated values can be used to construct the diagram shown in Fig. 14. His magnitude scale, which is much closer to the modern one than those of other astronomers of his time, is based on diameter measurements. The distribution is Gaussian, as was also found by Lundmark (1927) and Hubble and Humason (1931). Wirtz, using the measurements of Fath (1914), points out the shortcomings, unavoidable at this early stage of investigations:

``The luminosity curve cannot yet be transformed to unit space. Among other things, the limit of the observed space is not known, irrespective of the way of fixing the absolute measuring scale.''

Figure 14. A reconstruction of the first luminosity function (Wirtz 1926). ``While the distribution function of the apparent total magnitudes shows a considerable scatter and skewness, a much smaller scatter is obtained for the absolute magnitudes and a much closer approximation to the symmetrical curve. The luminosity function would then be to a first approximation a Gaussian error curve.''

While the luminosity function (LF) determined by Hubble and Humason (1931) is a Gaussian distribution of absolute magnitudes for the cluster nebulae, an asymmetric curve is found for isolated nebulae. The authors consider the latter effect to be at least partly due to selection. The original LF is shown in Fig. 15. The LF was also considered Gaussian by numerous subsequent authors (including Zwicky in 1933), at least, it was assumed that the LF has a maximum at a certain luminosity.

Figure 15. Hubble and Humason's (1931) luminosity function. ``Frequency distribution of absolute photographic magnitudes among extragalactic nebulae as derived from cluster (circles) and from isolated nebulae (dots). Distances of the isolated nebulae were derived mainly from red-shifts. The range in the two curves is the same. The asymmetry in the curve for isolated nebulae is believed to be due, in part at least, to effects of selection.''

An exponential luminosity function was given by Zwicky (1957):

Figure 16. Abell's (1962) luminosity function.

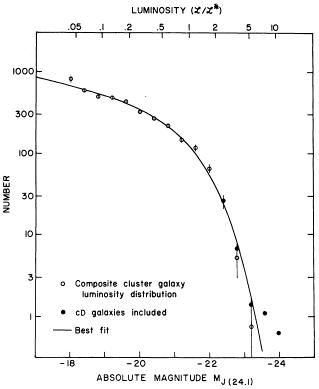
Figure 17. Schechter's (1976) luminosity function. ``Best fit of analytic expression to observed composite cluster luminosity distribution. Filled circles show the effect of including cD galaxies in composite.''

Other LFs were to follow, e.g. Abell's luminosity function shown in Fig. 16 (see also references in Schechter 1976). What was to become known as the Schechter function is double exponential when expressed in terms of absolute magnitude (Fig. 17):

``We investigate the expression

where , L, and are parameters to be determined from the data. The parameter is a number per unit volume, and L is a `characteristic luminosity' (with an equivalent `characteristic magnitude', M) at which the luminosity function exhibits a rapid change in the slope in the (log , log L)-plane. The existence of such a characteristic magnitude has long been stressed by Abell (1962, 1965 - his LF is the approximation of the measured distribution by two lines of different slope, intersecting at M), and his notation M has been pirated for the present discussion. The dimensionless parameter gives the slope of the luminosity function in the (log , log L)-plane when L << L.''

Recently, evidence has been accumulated by Sandage et al. (1985), that the Schechter function is the envelope of the individual Gaussian distributions of galaxies in different luminosity classes, possibly excepting very faint dwarf galaxies.