Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

3.3. Arguments for Baryonic Dark Matter

The cosmological nucleosynthesis argument is a two-edged sword: It requires both baryonic and nonbaryonic dark matter (Pagel 1990). This is because the value of _b allowed by Equation (3.1) almost certainly exceeds the density of visible baryons _v. A careful inventory by Persic & Salucci (1992) shows that the contributions to _v are 0.0007 in spirals, 0.0015 in ellipticals and spheroidals, 0.00035 h^-1.5 in hot gas within an Abell radius for rich clusters, and 0.00026 h^-1.5 in hot gas out to a virialization radius in groups and poor clusters. This gives a total of (2.2 + 0.6 h^-1.5) × 10^-3, so Equation (3.1) implies that the fraction of baryons in dark form must be in the range 70%-95% for 0.5 < h < 1. Note, however, that the Persic-Salucci estimate does not include any contribution from low surface brighteners galaxies (McGaugh 1994) or dwarf galaxies (Bristow & Phillipps 1994).

The discrepancy between _b and _v could be resolved if there were an appreciable density of intergalactic gas. We know there must be some neutral gas in the form of Lyman- clouds, but the density parameter associated with the "damped" clouds is probably no more than 0.003 h^-2 (Lanzetta et al 1991) - comparable to the density in galaxies, and consistent with the idea that these are protogalactic disks. Although the missing baryons could conceivably be in the form of a hot intergalactic medium (either never incorporated into galaxies or expelled by supernovae and galactic winds), the temperature would need to be finely tuned (Barcons et al 1991). The Gunn-Peterson test requires (HI) < 10^-8 h^-1 (Sargent & Steidel 1990), while the COBE limit on the Compton distortion of the microwave background (y < 3 × 10^-5) requires that, for a temperature T at redshift z,

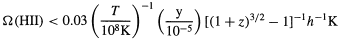
(3.2)

(Mather et al 1994). The latter limit implies that a smooth intergalactic medium (IGM) cannot generate the observed X-ray background, although there is still a temperature range between 10⁴ K and 10⁸ K in which one could have _IGM ~ _b. Whether one could expect so much gas to remain outside galaxies depends on its thermal history (Blanchard et al 1992).

The other possibility is that the missing baryons are inside galactic halos. The halo (lark matter cannot be in the form of hot gas for it would generate too many X-rays. Recently, however, Pfenniger et al (1994) have argued that it could be in the form of cold molecular gas. In their model, the gas is initially in the form of dense cloudlets with mass 10^-3 M and size 30 AU in a rotationally supported disk. The cloudlets then build up fractally to larger scales. Their model is motivated by the claim that spirals evolve along the Hubble sequence from Sd to Sa and that their mass-to-light ratio decreases in the process, which requires that the dark matter be progressively turned into stars. It also explains why the surface density ratio of dark matter and HI gas is constant outside the optical disk (Carignan et al 1990).

The final possibility-and the one that is the focus of the rest of this review - is that the dark baryons have been processed into stellar remnants. Even if stellar remnants have enough density to explain the alleged dark matter in the Galactic disk, this would be well below the value required by Equation (3.1), for if all disks have the 60% dark component envisaged for our Galaxy by Bahcall et al (1992a), this only corresponds to _v ~ 0.001. The more interesting question is whether the baryonic density could suffice to explain the dark matter in galactic halos; the term "Massive Compact Halo Object" or "MACHO" has been coined in this context. If our Galaxy is typical, the density associated with galactic halos would be _h 0.01 h^-1 (R_h / 35 kpc) where R_h is the halo radius. [The mass-to-light ratio for our Galaxy is (14-24) (R_h / 35 kpc) (Fich & Tremaine 1991) corresponding to _h = (0.008-0.014)h^-1 (R_h / 35 kpc); a more precise calculation would involve integrating over galaxies of all masses but then one would need to know the mass-dependence of R_h (Ashman et al 1993).] Thus Equation (3.1) implies that all the dark matter in our halo could be baryonic only for R_h < 50 h^-1 kpc. We saw in Section 2.2 that the minimum size of our halo is 70 kpc, which would just be compatible with this. If it is larger, the baryonic fraction could only be (R_h/50 h^-1 kpc)^-1. The cluster dark matter has a density _c 0.1 and Equation (3.1) implies that this matter cannot be purely baryonic unless one invokes inhomogeneous nucleosynthesis.

We note that there is no necessity for the Population III stars to form before galaxies just as long as some change in the conditions of star formation makes their mass different from what it is today. However, the epoch of formation will be very important for the relative distribution of baryonic and nonbaryonic dark matter, especially if the nonbaryonic dark matter is "cold" so that it can cluster in galactic halos. In this case, if the Population III stars form before galaxies, one might expect their remnants to be distributed throughout the Universe (White & Rees 1978), with the ratio of the baryonic and nonbaryonic densities being the same everywhere and of order 10. If they form at the same time as galaxy formation, perhaps in the first phase of protogalactic collapse, one would expect the remnants to be confined to halos and clusters. In this case, their contribution to the halo density could be larger since the baryons would probably dissipate and become more concentrated. Angular momentum considerations suggest that the local baryon fraction must be increased by at least a factor of 10 (Fall & Efstathiou 1981). If the WIMPs are hot and cannot cluster in halos, then halos would consist exclusively of MACHOs. These possibilities are illustrated in Figure 1.

Figure 1. The relative contributions of WIMPs and MACHOs to the halo density in various scenarios. Halos can consist exclusively of WIMPs only if the dark baryons are in a hot intergalactic medium and they can consist exclusively of MACHOs only if the WIMPs are hot. The most natural hypothesis is that they contain both.