Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

7.5. Line-to-Continuum Effects of Quasars

In some circumstances, only part of the quasar may be microlensed. In particular, the line and continuum fluxes may be affected differently because they may come from regions that act as extended and pointlike sources, respectively. [For a lens at a cosmological distance, the Einstein radius is 0.05(M/M)^1/2 h pc, whereas the size of the optical continuum and line regions are of order 10^-4 pc and 0.1-1 pc, respectively.] This effect can be used to probe individual sources. For example, the variations in the line-to-continuum ratio for different images of the same macrolensed quasar can be used to constrain the mass of the objects in the lensing galaxy. Evidence for such an effect may already exist in the case of the double quasar 2016+112, where variations in the intensity ratios for the different images suggest that the lensing objects have a mass in the range 3 × 10⁴ M to 3 × 10⁷ M (Subramanian & Chitre 1987).

The line-continuum effect can also show up in statistical studies of many quasars and there is one particularly important effect in this context. One would expect the characteristic equivalent width of quasar emission lines to decrease as one goes to higher redshift because there would be an increasing probability of having an intervening lens. Indeed, a third of quasars should have equivalent widths smaller by 2-3 at only a moderate redshift if _C = 1. This idea was first studied by Canizares (1982). More recently, Dalcanton et al (1994) have compared the equivalent widths for a high and low redshift sample comprising 835 Einstein Medium Source Survey quasars and 92 Steidel-Sargent absorption systems and find no difference. They infer the following limits:

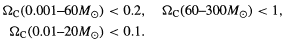
(7.2)

The mass limits come from the fact that the amplification of even the continuum region would be unimportant for M < 0.001 M, while the amplification of the broad-line regions would be important (cancelling the effect) for M > 20 M if _c = 0.1, for M > 60 M if _c = 0.2 or for M > 300 M if = 1. (These limits are indicated in Figure 5). This compares with the earlier Canizares (1982) constraint of _C(0.01-10⁵ M) < 1; his upper mass limit was larger because the size of the broad-line region was thought to be larger then. Note that Equation (7.2) is incompatible with Hawkins' claim that _C(10^-3 M) ~ 1, although one would only need to reduce _C or M slightly.