


The inhomogeneity of the Universe has been a major aspect of cosmology over the last 25 years. We have learned a great deal, especially from redshift surveys, and although things turn out to be fairly complicated in the sense that the Universe is not simple a pile of clusters distributed at random, nevertheless possesses some systematics upon which we can build models. The structures we have seen on the largest scales seem to be traced equally by galaxy samples drawn from quite different catalogues: optical catalogues (de Lapparent et al., 1986, 1988), infrared catalogues (Babul and Postman, 1990) or even catalogues of dwarf galaxies (Thuan et al, 1991).
In this section, I review the observed character of the clustering and the various attempts that have been made to quantify those visual impressions. Inevitably, much of the interpretation is predicated on notions developed through theories so it is almost impossible to discuss the observational data without reference to the theory! The theory comes in the following section. However, I shall try to provide interpretations of the data that are largely model independent.
Before discussing the data, we need a few basic notions such as correlation functions, bias parameters and the like. This subsection introduces these at a simple level, they are discussed in more detail later on.
2.1.1. 2-Point Correlation Functions
The two-point clustering correlation function has been the mainstay of clustering studies for over fifteen years. Its importance in cosmology has been fully discussed by Peebles (LSSU: 1980).
The 2-point correlation function as used in astrophysics describes one way in which the actual distribution of galaxies deviates from a simple Poisson distribution. There are other descriptors like three point correlation functions, the topological genus and so on; we shall come to those in more detail below (Section 3).
There are two sorts of 2-point function. One describing the
clustering as projected on the sky, thus describing the angular
distribution of galaxies in a typical galaxy catalogue. This is called
the angular 2-point correlation function and is generally denoted by
w( ). The other
describes the clustering in space and is called
the spatial 2-point correlation function. We frequently omit the word
"spatial". The (spatial) 2-point correlation function is generally
denoted by
). The other
describes the clustering in space and is called
the spatial 2-point correlation function. We frequently omit the word
"spatial". The (spatial) 2-point correlation function is generally
denoted by
 (r).
(r).
In order to provide a mathematical definition of the correlation function we will only consider the spatial 2-point function, the definition of the angular function follows similarly.
Consider a given galaxy in a homogeneous Poisson-distributed sample
of galaxies, then the probability of finding another galaxy in a small
element of volume  V
at a distance r would be
V
at a distance r would be
 P =
n
P =
n V, where
n is the
mean number density of galaxies. If the sample is clustered then the
probability will be different and will be expressible as
V, where
n is the
mean number density of galaxies. If the sample is clustered then the
probability will be different and will be expressible as
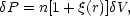
| (28) |
for some function
 (r)
satisfying the conditions
(r)
satisfying the conditions
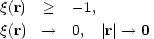
| (29) |
The first condition is essential since probabilities are positive, and the second is required in order that a mean density exist for the sample.
It is customary to make the assumption that the two point function is isotropic: it depends only on the distance between two points and not the direction of the line joining them:
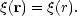
|
This is a reasonable but untested hypothesis.
In practice, the correlation function is estimated simply by counting the number of pairs within volumes around galaxies in the sample, and comparing that with the number that would be expected on the basis of a Poisson distributed sample having the same total population. There are subtleties however due to the fact that galaxies lying near the boundary of the sample volume have their neighbours censored by the bounding volume.
One method discussed by Rivolo (1986) is to use the estimator
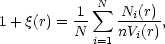
| (30) |
where N is the total number of galaxies in the sample and
n is their
number density. Ni(r) is the number of galaxies
lying in a shell of
thickness  r from
the ith galaxy, and Vi(r) is the volume
of the shell
lying within the sample volume. (So Ni(r) is
being compared with
nVi(r), the Poisson-expected number lying in
the shell). Note that n
is usually taken to be the sample mean, but if there is an alternative
(and better) way of estimating the mean density, the alternative
should be used.
r from
the ith galaxy, and Vi(r) is the volume
of the shell
lying within the sample volume. (So Ni(r) is
being compared with
nVi(r), the Poisson-expected number lying in
the shell). Note that n
is usually taken to be the sample mean, but if there is an alternative
(and better) way of estimating the mean density, the alternative
should be used.
An alternative strategy to calculating
 (r) for a
catalogue of NG
galaxies is to put down NR points at random in the
survey volume and
compare the number of pairs of galaxies nGG(r)
having separation r
with the number of pairs nRG(r) consisting of a
random point and a galaxy, separated by the same
(r) for a
catalogue of NG
galaxies is to put down NR points at random in the
survey volume and
compare the number of pairs of galaxies nGG(r)
having separation r
with the number of pairs nRG(r) consisting of a
random point and a galaxy, separated by the same
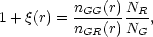
| (31) |
(Davies et al. 1988).
(As an aside it is worth commenting that some authors (eg.
Pietronero, 1987)
have advocated using a "structure function" for a
distribution of N galaxies situated at points
ri :
 (r) =
N1
(r) =
N1  n(r + ri). This is analogous to the
correlation function, but has the
claimed advantage that it does not depend explicitly in its
calculation on the mean density for the sample. The value of the
function is however strongly density dependent, as can be seen for a
Poisson distribution where
n(r + ri). This is analogous to the
correlation function, but has the
claimed advantage that it does not depend explicitly in its
calculation on the mean density for the sample. The value of the
function is however strongly density dependent, as can be seen for a
Poisson distribution where
 (r) = 0 and
(r) = 0 and
 (r) =
(r) =
 . The idea
is that one
would be able to study the clustering without the assumption that the
universe is homogeneous. Given that there is considerable evidence
that the universe is indeed homogeneous in the large, this may seem
somewhat unnecessary.)
. The idea
is that one
would be able to study the clustering without the assumption that the
universe is homogeneous. Given that there is considerable evidence
that the universe is indeed homogeneous in the large, this may seem
somewhat unnecessary.)
The two point correlation function for the distribution of galaxies has a roughly power law behaviour on scales R < 10h-1 Mpc., with a slope of -1.77:
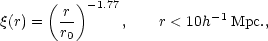
| (32) |
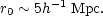
|
This is frequently referred to as "the 1.8 power law". What happens beyond 10h-1 Mpc, is somewhat contentious. It certainly falls below the power law behaviour, but it is not even clear whether it falls to negative values at any scale where it is measurable. What ig on the small scales and in particular how the small scale structures relate to one another. The inadequacy of the 2-point function in describing what is seen on the largest scales has motivated people to look at other ways of describing the large scale structure.
The accuracy with which the two-point correlation function is determined in redshift surveys has been questioned: Einasto, Klypin and Saar (1986) argued that r0 depended systematically on the depth of the sample, though this is probably a consequence of a bias introduced by luminosity segregation (Martínez and Jones, 1990).
Formally, the Power Spectrum of a distribution of points is defined as the Fourier transform of the two-point correlation function:
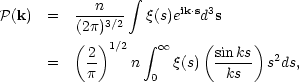
| (33) |
where the last equality follows because
 (r) =
(r) =
 (r) is
direction independent.
(k = |k|). These relationships are formally invertible,
so given
(r) is
direction independent.
(k = |k|). These relationships are formally invertible,
so given
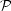 (k) it is
possible to get
(k) it is
possible to get
 (r).
(r).
So why introduce the power spectrum? The reason can be seen from the following argument. Suppose that the density of galaxies in a volume V is n(r), and that the mean of this is n (so the total number of galaxies is nV).
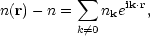
| (34) |
where the sum extends over all wavenumbers than fit in the volume. It can then be shown that
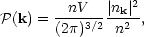
| (35) |
and that (by Fourier transform relationship between
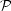 (k) and
(k) and
 (r)):
(r)):
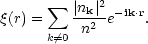
| (36) |
The distribution of the amplitudes of each Fourier component of the fluctuating density field is determined by the physical processes that generated the fluctuations in the first place. As long as the amplitudes are small and linear theory applies, the evolution of these Fourier components is independent and determined by the physical processes in the early universe. So decomposing the density field into a set of Fourier components is useful. What the power spectrum then tells us is the distribution of the mean square amplitudes of these components. The power spectrum is the contribution of each Fourier mode to the total variance of the density fluctuations.
The appearance of the
|nk|2 term is interesting. It tells us
that 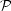 (k)
only contains information about the amplitudes of the Fourier
components of the fluctuating density field.
(k)
only contains information about the amplitudes of the Fourier
components of the fluctuating density field.
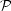 (k) contains no
phase information. Consequently, the 2-point correlation function does not
contain this information either. Many quite different distributions
can have the same power spectrum and correlation function. Consider
the example of a density field that is uniform on the faces of a cubic
lattice, and zero elsewhere. That can be written as a Fourier series
and the Fourier component have highly correlated phases. Randomize the
phases and the density distribution looks inhomogeneous and quite
disordered, yet the correlation function and power spectrum remain
unchanged.
(k) contains no
phase information. Consequently, the 2-point correlation function does not
contain this information either. Many quite different distributions
can have the same power spectrum and correlation function. Consider
the example of a density field that is uniform on the faces of a cubic
lattice, and zero elsewhere. That can be written as a Fourier series
and the Fourier component have highly correlated phases. Randomize the
phases and the density distribution looks inhomogeneous and quite
disordered, yet the correlation function and power spectrum remain
unchanged.
As a final technical point we should look at the concept of biasing that comes in when one wishes to compare the distribution of matter (some of which may be dark) with the distribution of luminous galaxies. Light does not necessarily trace mass and so the clustering properties of the light distribution may be quite different from the clustering properties of the mass distribution.
The need to relate the mass and light distributions arises in two situations. In the first place one may wish to make a comparison between the predictions of an N-body model for galaxy clustering with the observed distribution. At present the N-body models simply describe the distribution of the gravitating matter and some hypothesis is needed to say which material particles are luminous. Ideally, really sophisticated N-body models would incorporate details of the star formation process and make such a hypothesis unnecessary. In the second place, we may simply wish to infer the mass distribution from the observed light distribution in order to relate the observed velocity fields to the matter distribution that generated them.
It would be bizarre indeed if the distributions of mass and light were not related and the simplest hypothesis is that the fluctuations in the mass distribution are proportional to the fluctuations in the luminosity distribution:
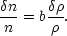
| (37) |
Here n represents the mean density of galaxies (the luminous
material)
and  n the
fluctuations in the galaxy density (which will be position
dependent).
n the
fluctuations in the galaxy density (which will be position
dependent).  represents the mean mass density and
represents the mean mass density and

 the fluctuations in mass density.
the fluctuations in mass density.
This assumption is probably a considerable simplification of the real physics, but we have to start somewhere. In fact, b is generally chosen to be a constant, independent of position or scale, but possibly dependent on the morphological type of galaxy that makes up the luminous sample. This is forced on us because whereas all galaxies seem to trace out the same large scale distribution, some are more clustered than others. For example, the elliptical galaxies seem to be more highly clustered than spirals (they occupy the denser regions of the universe). So the bias parameter for ellipticals must be somewhat larger than that for spirals.
The bias parameter plays a central role in relating the deviations from pure Hubble flow (which are driven by the total matter distribution) with measures of the clustering of galaxies (which depend on where the luminous material happens to be). It can be shown (see Peebles, LSSU equations (8.2) and (14.2)) that in linear theory the relationship between the peculiar velocity field v and the fluctuating gravitational force g is
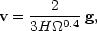
| (38) |
where, by virtue of the perturbed Poisson equation, the fluctuating
force g is related to the distribution of relative density
fluctuations  (x) =
(x) =

 /
/
 :
:
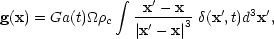
| (39) |
The mass density fluctuations

 /
/
 are supposed to be
related to the fluctuations
are supposed to be
related to the fluctuations
 n / n in
the observed galaxy density via the bias
parameter b defined above. So what we observe is
n / n in
the observed galaxy density via the bias
parameter b defined above. So what we observe is
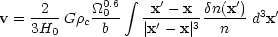
| (40) |
Note that there is a normalization factor
 00.6 / b to be
fitted when relating the variations in the luminosity with the peculiar
velocities. Note also that decreasing b increases v, for a
given luminosity distribution.
00.6 / b to be
fitted when relating the variations in the luminosity with the peculiar
velocities. Note also that decreasing b increases v, for a
given luminosity distribution.
The upshot of this is that methods for determining
 0 that
compare velocity fields with density fluctuations in fact only determine
0 that
compare velocity fields with density fluctuations in fact only determine
 0
b-5/3,
and we need to get b from somewhere else (usually a theoretical
prejudice based on an N-body model!).
0
b-5/3,
and we need to get b from somewhere else (usually a theoretical
prejudice based on an N-body model!).
Note that if we compare two different catalogues we can determine
 0
b-5/3, for each catalogue. The ratio of these gives us
the ratio of the bias parameters for the two catalogues
(Babul and Postman, 1990;
Lahav et al., 1990).
At least we can reassure ourselves that different
galaxy catalogues have different bias parameters!
0
b-5/3, for each catalogue. The ratio of these gives us
the ratio of the bias parameters for the two catalogues
(Babul and Postman, 1990;
Lahav et al., 1990).
At least we can reassure ourselves that different
galaxy catalogues have different bias parameters!