The Large Scale Structure of the Universe

4.4. Understanding Large Scale Structure

The numerical simulations certainly show how the large scale structures form, and they allow us to test different hypotheses regarding the initial spectrum, biasing, cosmological constants and whatever other parameters come into describing the universe. They do not however explain why the structure is the way it is. In other words, why do we see voids bounded by sheet-like structures? Until recently, the models were limited to several tens of thousands of particles, or at most 250,000. As impressive as this number seems, it still imposes a major limitation on our ability to resolve the structures on scales as small as galaxies while still looking at the largest structures. There is a lot of room for trying to develop a mathematical understanding of the process of structure formation.

The pioneering paper in this area was undoubtedly the work of Press and Schechter (1974, "PS") who through a very simple argument were able to calculate the mass spectrum of objects that form from a given spectrum of density fluctuations at the epoch of recombination. They argued that structure formation is a hierarchical process, the levels of which are determined by thresholding the density fluctuation field. The process stops when a limiting threshold is reached. At first, the limiting threshold was fixed by timescale arguments, but that idea was later changed when biasing was introduced as the mechanism whereby galaxies and clusters were discriminated as luminous objects (Kaiser, 1984; Bardeen, Bond, Kaiser and Szalay, 1986; see also Dekel and Rees, 1987).

The PS method is purely geometrical and is based only on knowing the fraction of the mass f(M) in the universe at recombination that has density contrast in excess of standard deviations, sigma _M, when the density field has been filtered with a window encompassing a mass M. (Note that sigma _M depends on mass). For Gaussian fluctuations in density:

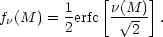
(66)

Note that in general will depend on the mass scale, as would happen in the case of constant delta rho / rho thresholding. Biased galaxy formation in its simple form only needs constant thresholding.

The number of objects in the mass interval M to M + dM is, according to the PS ansatz:

(67)

The first of these equations says that the numer of objects appearing in a given mass interval is simply the number of above threshold regions that appear when the window radius is changed. The factor 2 is a famous "fudge factor" included to account for infalling material. The second equation is merely a rewrite of the first, showing explicitly how the mass dependence of the threshold comes in.

The philosophy behind these equations is however flawed, as can be seen from numerical simulations of what the PS procedure is actually counting (Appel and Jones, 1990). Decreasing the window radius, for example, does not necessarily lead to the birth of objects whose mean size is known, most regions simply shrink in size as the window radius is increased.

The Press-Schechter method takes no account of the way in which gravity works on the mass distribution, or the way mass is converted into stars. Nevertheless, Efstathiou and Rees (1988) showed that, despite the naivety of the approach, the Press-Schechter formalism provided an acceptable fitting function to the mass function of objects identified in N-body experiments on the basis of a "friend-of-friends" algorithm. It should be noted that this way of identifying bound objects in N-body simulations is not in fact what is calculated by the PS threshold-based argument. In other words, the PS approach provides a pretty good fitting formula. (See also Carlberg and Couchman (1989)).

The subject has a long history (Couchman, 1987a, b; Martínez-González and Sanz, 1988; Lucchin and Matarrese, 1988; Appel and Jones, 1990; Peacock and Heavens, 1990; to name but a few). Appel and Jones (1990) presented a new definition for what an incipient galaxy should be when looking at a random density field. In their definition, the window radius should adapt itself as a function of position: the window radius is increased until the local density maximum disappears below some chosen threshold. That radius then defines (up to a constant of proportionality) the mass of the object. By construction when using this prescription, objects of small size are rarely embedded inside bigger objects, thus solving the "nesting problem".

The "nesting problem" is solved by Peacock and Heavens (1990) in an entirely different way, though like most other authors they accept the basic tenet that the number distribution is given by the change in the occupied volume f(M) with M.

A recent paper by Bond, Cole, Efstathiou and Kaiser (1991) looks at the way peaks in the density field appear and disappear as the window function radius is changed. In this sense the approach is rather like that of Appel and Jones (1990), but their treatment does not make the simplifying assumption that an object is defined by the disappearance of a peak when the window radius is increased. What is interesting is that, in their simplest model, they recover precisely the Press-Schechter formula!