Annu. Rev. Astron. Astrophys. 1994. 32: 153-90 Copyright © 1994 by Annual Reviews. All rights reserved

3.3. Observational Constraints

We have discussed how the r-process works in both primary and secondary scenarios and possible sites for the r-process. Let us turn now to the "observational" data to evaluate the plausibility of the proposed sites. These data will be astronomical, meteoritical, and nuclear.

We begin with the observations of old stars carried out by Sneden and collaborators (Sneden & Parthasarathy 1983, Sneden & Pilachowski 1985, Gilroy et al 1988; see also Wheeler et al 1989). These workers find that the elemental abundances, i.e. abundances as a function of Z, the proton number, of heavy elements in the atmospheres of these old stars match rather well the solar system r-process elemental abundances; s-process elemental abundances do not provide a good fit. One conclusion we may draw from this is that the r-process dominated the s-process at early times in our Galaxy. This would strongly suggest that the r-process is primary because a secondary r-process must produce r-nuclei from an already abundant population of s-nuclei. Another important conclusion is that the r-process mechanism has remained essentially the same throughout the Galaxy's history. A caveat to both of these conclusions is that they are based on elemental abundances, whereas a truly definitive identification of the heavy nuclei in old stars as r-process in origin would require isotopic abundances, information that spectroscopy cannot yet generally give us. Nevertheless, the evidence for a primary r-process that has operated in the same fashion throughout the Galaxy's history is compelling.

The next item of evidence we may consider is the question of the timescale for heavy element formation. Mathews & Cowan (1990) and Mathews et al (1992, 1993) have fit chemical evolution models to observations of the elemental abundances of europium (a mostly r-process element) and iron in the atmospheres of old stars. The only models that give good fits to the data are a primary r-process in type II and Ib (that is, core-collapse of a massive star) supernovae or a secondary r-process in which the neutron source itself is primary. An example of a primary neutron source in a secondary r-process event is the ¹³C produced by mixing of protons down into the helium shell for supernova shock-induced helium or carbon burning. This is effectively a primary source because the star itself constructs the ¹³C from its initial supply of protons and from ¹²C made during helium burning. Another example is the neutrino-induced r-process. The neutrons in this source come mostly from inelastic scatterings of neutrinos on ⁴He nuclei in the helium shell. The star itself produced almost all of the ⁴He nuclei, so the neutron source is primary. Other proposed sites seemingly ruled out by these timescale arguments are: tidal disruptions of neutron stars by black holes, neutron star-neutron star collisions, a secondary r-process with a secondary neutron source such as ²²Ne, neutron-star accretion disks (Hogan & Applegate 1987), core helium flash in low-mass stars (Cowan et al 1982), and classical novae (Hoyle & Clayton 1974).

Experimental nuclear physicists have also provided us with important clues about the r-process. In particular, K.-L. Kratz and collaborators have measured the beta-decay lifetimes of r-process "waiting pointing" nuclei on the N = A - Z = 50 and N = 82 closed neutron shells (Kratz et al 1988, 1990). These nuclei have particularly strongly bound valence neutrons. Now the total abundance of the element Z is a sum over the abundances of all of the isotopes of that element:

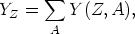
(6)

The average rate of beta-decay flow out of element Z is

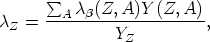
(7)

where (Z, A) is the beta-decay rate of nucleus (Z, A). The abundance Y_Z decreases during the r-process by beta decay out of Z into Z + 1 and increases by beta decay into Z from Z - 1; thus,

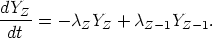
(8)

Where the r-process path crosses the N = 50 and N = 82 closed shells, a single isotope dominates the abundances because of the strong neutron binding. For these nuclei, Y_Z Y(Z, Z + 50) for the N = 50 closed neutron shell and Y_Z Y(Z, Z + 82) for N = 82. If the conditions for (n,) - (, n) equilibrium hold for a long enough time, the system will achieve approximate steady beta flow such that dY_Z/dt 0. In this case _Z Y_Z constant. What is particularly significant is that the decay rates found by Kratz and co-workers times the appropriate abundances along the closed neutron shells as inferred directly from the solar system r-process data show that _Z Y_Z is approximately constant for the N = 50 and N = 82 waiting-point nuclei. This is strong, albeit circumstantial, evidence that the r-process achieved the conditions of (n,) - (, n) equilibrium and steady beta flow. This would indicate that the r-process is primary since a secondary r-process does not achieve (n,) - (, n) equilibrium. Another important result found from this work is that the constant _Z Y_Z for the N = 50 closed neutron shell is different from that for the N = 82 closed shell. The r-process did not achieve global steady beta flow (Kratz et al 1993). We interpret this to mean that the r-process abundance distribution actually results from a sum of components resulting from a varying set of r-process conditions - no single set of conditions gives rise to the solar system abundance curve. While this point was long appreciated by theoreticians (Seeger et al 1965, Kodama & Takahashi 1975, Hillebrandt et al 1976), the work of Kratz and collaborators establishes this result directly from nuclear physics and meteoritic abundances. The actual r-process site in nature must naturally give rise to a varying set of r-process conditions.

The final observational constraint we consider is the mass of r-process material in the Galaxy. From meteorites and abundances in the Sun we can infer that the mass fraction of r-nuclei in the Galaxy is 2 × 10^-7 (from the data in Anders & Grevesse 1989). If the mass of our Galaxy is 1.5 × 10¹¹ M, there are some 10⁴ M of r-process material in our Galaxy. Now the rate of supernovae in our Galaxy is between 0.1 yr^-1 and 0.01 yr^-1 (e.g. Tammann 1982, Van den Bergh & Tammann 1991) and the Galaxy is of order 10¹⁰ years old; therefore, there have been some 10⁸ to 10⁹ supernovae in our Galaxy's history. If each of these supernovae produced r-process material, we expect each supernova to make 10^-5 to 10^-4 M of r-nuclei. This is a tiny fraction of the total mass ejected in a supernova and its smallness provides an important constraint on the site of the r-process.

From the astronomical and nuclear observations, we have found that the r- process is likely a primary event occurring in core-collapse supernovae. If the r-process comes from low entropy, neutron-rich material ejected from the core in a supernova, then we know from the discussion in Section 2.1 that we need material with Y_e 0.2 to make actinide nuclei. Such material must come from fairly deep in the core. Hillebrandt et al (1976) found that a supernova needs to eject of order 0.1M of material to get Y_e 0.1 - 0.2 material out of the core. Such a large amount would overproduce the r-nuclei by a factor of 10³ if all supernovae ejected this much neutron-rich matter. It may be that only rare supernovae, such as those with high magnetic fields and rotation rates (LeBlanc & Wilson 1970, Meier et al 1976, Muller & Hillebrandt 1979, Symbalisty 1984, Symbalisty et al 1985), can eject neutron-rich matter. It remains to be seen, however, whether the high magnetic fields and/or rotation rates in these scenarios are indeed achieved in nature. In conclusion, we have no natural scenario for a low entropy primary r-process that yields 10^-4 M of r-process material per event. Fortunately, we do have a high entropy r-process that gives this yield of r-nuclei per supernova. We turn to this scenario in the next section.