To speak of the "dark matter" problem is to beg one of the most important
conundrums in present-day science; after all we have no direct
evidence that dark matter actually exists in appreciable quantities.
All we know is that the masses directly observed in galactic systems
fall below
what is calculated using standard dynamics. Stuffing galactic systems
and the universe with putative dark matter is perhaps the least
painful remedy for most people,
but it is not the only one possible. Another avenue
worthy of consideration builds on a possible failure of standard dynamics
under the conditions that prevail in galactic systems.
As you may know, the modified dynamics (MOND) has been put forth in just
this vein
[1].
It hinges on the accelerations in galactic
systems being very small compared with what is encountered in the solar
system, say. MOND asserts that non-relativistic dynamics involves the
constant
a0, with the dimensions of acceleration, so that in
the formal limit a0
0 - i.e.,
when all quantities with the dimensions of acceleration are much larger
than a0-standard dynamics obtains (in analogy with the
appearance of 
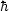in
quantum mechanics, and the classical limit for
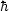
0).
In the opposite (MOND) limit of large
a0 dynamics is marked by reduced inertia;
one may roughly say that in this limit inertia at acceleration a is
ma2 / a0, instead of the standard
ma. This still allows for different specific formulations. Indeed
we have nonrelativistic
formulations of MOND, derivable from actions, based on either modified
gravity
[2],
or on modified inertia
[3];
these will be described below.
A simple, if primitive, formulation that captures
much of the content of MOND, and which gives the basic idea, is this:
Imagine a test particle in the gravitational field
of some mass distribution whose standard (Newtonian) gravitational
acceleration field is
gN. In standard dynamics the acceleration, g,
of the particle is
gN itself. MOND posits that this is so only in the limit
gN >> a0. In the opposite limit
gN << a0 we have roughly
g ~ (gN a00)1/2.
To interpolate between the limits we use a relation of the form
µ(g / a00)g =
gN, where µ(x)
x for x
<< 1, and µ(x)
1 when x
>> 1.
This relation gives an approximate relation between the typical
accelerations
in a system (as embodied, say, in an exact virial relation derived from an
exact theory). It also gives a very good approximation for the acceleration
in circular motion relevant for rotation curves of disc galaxies
[3]
[4]
(in modified inertia theories it give the exact rotation curve).
In the more decent formulations of MOND, the actual acceleration of
a test particle is
not directly related to the local Newtonian acceleration as in the above
relation (in particular, the two are not in the same direction, in
general).
Some immediate, and unavoidable, predictions of even the basic tenets are [1] [5]:
1. The rotation curve for any isolated body becomes flat, asymptotically.
2. The asymptotic rotational velocity,
V
,
depends only on the total mass of the body, M, via
V4
= MGa0. This predicts a Tully-Fisher relation
between velocity and luminosity
if the M / L values are narrowly distributed.
3. A similar approximate relation exists,
for a body supported by random motions,
between the mean velocity dispersion and the total mass.
This is relevant to mass determinations of systems such as
dwarf-spheroidal, and elliptical, galaxies, and of galaxy
groups and clusters. It also predicts an approximate
L 
4 relation in
such systems (with similar M/L values).
4. The smaller the typical acceleration of a gravitationally bound system, the larger the mass discrepancy it should evince. It had thus been predicted that all low-surface-brightness (LSB) systems should evince large mass discrepancies since, for a given M/L, surface brightness is proportional to acceleration (in the mean). This pertains, e.g., to dwarf-spheroidal satellites of the Milky Way, and to low-surface-brightness disc galaxies.
5. Above all, the full rotation curve of a disc galaxy should be obtained, using MOND, from the distribution of the observed mass alone.
Comparison with the data, as discussed later, yields a value of a0, determined in several, independent ways (using the different roles of a0 in the theory). Very interestingly, the value a0 turns out to be of the same order as c H0 - an acceleration parameter of cosmological significance [1]. Anticipating later discussion, I remark here that this might be a crucial clue as to the origin of MOND, and its possible origin in effects related to cosmology.