


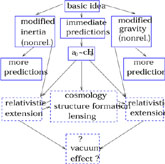
Those cleaving to Newtonian dynamics may take the success of MOND to reflect some very strict regularity-encompassing the whole gamut of galactic systems-relating the distribution of visible matter to that of dark matter via a simple formula. The few of us who have contributed to MOND theory and testing over the years view this success as strong indication of departure from standard dynamics in the parameter region relevant to galactic systems. Taking MOND in such a vein, one seeks to construct theories, with increasing depth and compass, that incorporate the basic tenets of MOND. Figure 3 presents the schematics of these efforts, with full-line blocks marking areas in advanced stages of development.
|
Figure 3.Schematics of the MOND program. |
At the nonrelativistic level, at least, MOND may be viewed as either a
modification of gravity, or a modification of inertia
[1].
In the former, the gravitational field produced by a given mass distribution
is dictated by a new equation; in the latter the equation of motion is
MONDified, while the force fields remain intact.
An example of the former is the MONDification of the Poisson equation
discussed in ref.
[2]
where the gravitational potential,
 , is
determined by the mass distribution,
, is
determined by the mass distribution,
 , via
, via
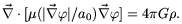
| (1) |
Mondified inertia is discussed in refs.
[3]
[25]. In such
theories, when derived
from an action, one replaces the standard kinetic action for a particle
( v2 / 2 dt) by a kinetic action
that is a more complicated functional of the particle trajectory
v2 / 2 dt) by a kinetic action
that is a more complicated functional of the particle trajectory
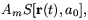
| (2) |
where Am depends only on the body, and can be
identified with its mass,
and S depends only on the trajectory and on a0
as a parameter. Weak equivalence is thus insured. In the formal limit
a0
 0
the action goes to the standard kinetic action. In the opposite limit,
a0
0
the action goes to the standard kinetic action. In the opposite limit,
a0

 ,
S
,
S  a0-1, and inertia disappears in the very limit.
a0-1, and inertia disappears in the very limit.
With respect to Newtonian dynamics, special relativistic dynamics is an
example of modified inertia:
The equation of motion of a relativistic particle moving in a force field
F(r) is
md ( v /
dt =
m
v /
dt =
m [a +
[a +
 2
c-2(v . a)v] =
F(r), derived from the kinetic action
mc2
2
c-2(v . a)v] =
F(r), derived from the kinetic action
mc2
 d
d =
mc2
=
mc2

 -1 dt.
Here too there appears a parameter, c, which, like
a0 in MOND (and
-1 dt.
Here too there appears a parameter, c, which, like
a0 in MOND (and
 in QM) both delimits the
standard (classical)
region, and enters the dynamics in the non-classical regime.
Unlike the special-relativistic action, which is still local, the MOND
action is perforce non-local if it is to be Galilei invariant
[3].
in QM) both delimits the
standard (classical)
region, and enters the dynamics in the non-classical regime.
Unlike the special-relativistic action, which is still local, the MOND
action is perforce non-local if it is to be Galilei invariant
[3].
Mondified gravity and mondified inertia do not differ on what we call
the basic predictions of MOND:
The asymptotic flatness of rotation curves (and their general shape),
the M  V4 relation, the added stability of systems in the
deep MOND regime
[26],
etc. There are, however, important differences; some examples are:
1. In mondified gravity only systems governed by pure gravity (such as
galactic systems) are affected, while in mondified inertia the
modification applies for whatever combination of forces is at play.
2. in the former, the acceleration of a test particle depends only
on its position in the field, while in the latter it depends strongly on
other
details of the trajectory (inertia is identified with acceleration only in
standard Newtonian dynamics). As an example, we can see in the
special-relativity case, mentioned above, that the
v . a term vanishes for a circular
orbit, but dominates, at high
V4 relation, the added stability of systems in the
deep MOND regime
[26],
etc. There are, however, important differences; some examples are:
1. In mondified gravity only systems governed by pure gravity (such as
galactic systems) are affected, while in mondified inertia the
modification applies for whatever combination of forces is at play.
2. in the former, the acceleration of a test particle depends only
on its position in the field, while in the latter it depends strongly on
other
details of the trajectory (inertia is identified with acceleration only in
standard Newtonian dynamics). As an example, we can see in the
special-relativity case, mentioned above, that the
v . a term vanishes for a circular
orbit, but dominates, at high
 , for a linear trajectory.
3. In mondified inertia the expressions for the conserved quantities and
adiabatic invariants in terms of the motion are modified
[3], in
contradistinction to mondified gravity.
, for a linear trajectory.
3. In mondified inertia the expressions for the conserved quantities and
adiabatic invariants in terms of the motion are modified
[3], in
contradistinction to mondified gravity.
An acceptable relativistic extension for MOND is not yet at hand. Discussions of various candidates can be found in refs. [2] [27] [28] [29], but each of these has its problems. These problems seem to be specific to the particular models (e.g. that in [2] has superluminal modes, scalar-tensor theories as discussed in [28] do not give as large a light bending as is observed, and that in [29] is based on a non-dynamical pregeometry).
Reflection over this question has convinced me that a relativistic extension
will not just be a relativistic theory where a0
appears as a parameter, with GR restored in the limit a0
 0. I have
always viewed MOND as an
effective theory (i.e. an approximate theory that results from a deeper one
in a certain limit, and/or when some of the relevant degrees of freedom
are integrated out). In the present case MOND is perhaps an approximation
in the limit of small sizes and short times (on the cosmological scale),
and nonrelativistic motion, due to some yet-undiscovered effect
connected with cosmology.
An analogy will highlight the point: If we are ignorant of earth gravity
as derived from the pull of the earth-such as when we are immured forever
in a small laboratory near the earth's surface-dynamics is described
approximately by modified inertia of the form
0. I have
always viewed MOND as an
effective theory (i.e. an approximate theory that results from a deeper one
in a certain limit, and/or when some of the relevant degrees of freedom
are integrated out). In the present case MOND is perhaps an approximation
in the limit of small sizes and short times (on the cosmological scale),
and nonrelativistic motion, due to some yet-undiscovered effect
connected with cosmology.
An analogy will highlight the point: If we are ignorant of earth gravity
as derived from the pull of the earth-such as when we are immured forever
in a small laboratory near the earth's surface-dynamics is described
approximately by modified inertia of the form
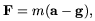
| (3) |
where F is the applied force excluding earth gravity, and g is the free-fall acceleration on earth. This can be recast to resemble MOND inertia:
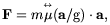
| (4) |
where
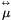
 1 - [e
1 - [e
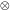 x] /
x2, and e
x] /
x2, and e
 g / g is
a down-pointing unit vector.
This is a good approximation inasmuch as this proverbial
laboratory is our whole universe; i.e., for systems small compared with
R
g / g is
a down-pointing unit vector.
This is a good approximation inasmuch as this proverbial
laboratory is our whole universe; i.e., for systems small compared with
R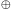 (analogous to the Hubble distance), and times small compared with
H
(analogous to the Hubble distance), and times small compared with
H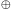 -1
= t
-1
= t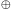
 R
R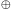 /
c
/
c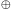 ,
where
c
,
where
c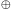 =
(M
=
(M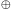 G
/ R
G
/ R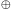 )1/2 is the escape speed-analogous
to the speed of light.
The effective "acceleration constant", g, appearing
in this modified inertia is
related to the "cosmological" parameters by g =
c
)1/2 is the escape speed-analogous
to the speed of light.
The effective "acceleration constant", g, appearing
in this modified inertia is
related to the "cosmological" parameters by g =
c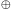 H
H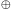 .
.
In a relativistic extension of MOND, or in the cosmological
context, a0 may lose its role as a
"universal constant"
[3]
[25]
- as g does in the above
analogy when dealing with, say, satellite motion for which v ~
c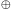 . The
peculiar situation is further highlighted by the fact that - in view of
a0 ~ cH0 - the
only system that is both high-field in the GR sense
and in the deep-MOND regime is the universe at large.
(In the quantum analogue a system in the high-field, quantum regime is of
Planck scale or smaller. There, we can, at least look from outside the
Planck scale, which we cannot do in MOND.) Relativistic
MOND must then be understood as part and parcel of cosmology, as I
elaborate more in the next section.
. The
peculiar situation is further highlighted by the fact that - in view of
a0 ~ cH0 - the
only system that is both high-field in the GR sense
and in the deep-MOND regime is the universe at large.
(In the quantum analogue a system in the high-field, quantum regime is of
Planck scale or smaller. There, we can, at least look from outside the
Planck scale, which we cannot do in MOND.) Relativistic
MOND must then be understood as part and parcel of cosmology, as I
elaborate more in the next section.