Why should then a cosmological acceleration parameter enter local dynamics in galaxy systems? I have discussed this question in refs. [3] [25] and give here a brief account. I shall concentrate on mondified inertia, which seems to me more promising at this juncture.
The thread I would like to follow is that inertia might result from the
interaction of matter with the vacuum. Also, cosmology affects the
vacuum and is affected by it (e.g. through a contribution to a cosmological
constant).
So, either cosmology affects inertia through the intermediary vacuum,
or, cosmology and inertia are both affected by the vacuum dynamics, which
then enters cosmology, say, as a cosmological constant,
, and MOND through
a0 
c
1/2.
Inertia is what makes kinematics into dynamics, associating with motion the attributes of energy and momentum that can be changed only by applying forces, as described by the appropriate equation of motion. Just how much energy and momentum is associated with so much motion is dictated by the kinetic action of the relevant degrees of freedom. To obtain inertia as a derived effect is to derive the kinetic actions (in our case from some vacuum effect). From this action the energy-momentum tensor is derived; thus, in relativity, this action also encapsules the contribution of the particular degree of freedom to the sources of gravity. Attempts to derive inertia-in the spirit of Mach's principle-have concentrated mainly on inertia of bodies-see e.g. ref. [33]. But, of course, all dynamical degrees of freedom, whether we describe them as bodies (particles) or fields, carry inertia.
Supposedly one starts from only interactions between the different degrees of freedom and get inertia in the form of effective kinetic actions. We know that interactions can, indeed, induce and modify inertial actions. For example, the effective mass of "free" electrons and holes in a semiconductor can be greatly changed from its vacuum value; mass renormalization in field theory is, of course, a vacuum effect; and the Higgs mechanism induces an effective mass term from the interaction with the putative Higgs field. It is also known that the interaction of the electromagnetic field with charged vacuum fields begets a free effective action for the electromagnetic field-the Heisenberg-Euler effective action (see e.g. [34] and [35] p. 195). What role, if any, these mechanisms play in MOND is not clear. However, since they are known to affect inertia, they must be reckoned with in any complete analysis.
The scheme I have in mind is inspired by Sakharov's proposal
[36]
to derive the "free" (Einstein-Hilbert) action of gravity from effects of
the vacuum: Curvature of space-time modifies the dynamical behavior of
vacuum fields, hence producing an
associated energy or action for the metric field. To lowest order (in the
Planck length over the curvature radius) this gives the desired expression
g1/2R. Sakharov's
arguments make use of the fact that the vacuum fields have inertia (since
they are assumed to carry the usual energy-momentum). So, derived inertia
comes prior to induced gravity a-la Sakharov. Mechanisms proposed in the
literature to produce inertia from vacuum effects (as in refs.
[37]
[38])
also presuppose inertia of the vacuum fields, and can thus not serve
as primary mechanisms for inertia.
For the vacuum to be an agent for inertia it is necessary, in the first
place, that a non-inertial observer be able to perceive enough
details of its motion in the vacuum. The Lorentz invariance
built into our theories leads to a vacuum that is,
perforce, Lorentz invariant, so uniform motion cannot be detected
through it.
It is well known, however, that non-inertial motion raises from the vacuum
a specter that can be sensed by the observer in different ways
[39].
This phenomenon
has so far been studied for only a limited class of simple motions.
For example, for an observer on a collinear trajectory of
constant-acceleration, a, (hyperbolic motion) this avatar of the
vacuum is the Unruh radiation: a thermal bath the observer finds itself
immersed in,
of temperature T = a /
2
(
= 1, c = 1,
k = 1)
[39]
[40].
Circular, highly relativistic motions have been discussed, e.g. in refs.
[41] -
[46]
where it is found that a single parameter,
a = 
2
v2 / r
2 / r,
still determines the spectrum of the incarnation of the vacuum
( is the Lorentz
factor); this is quasi-thermal with effective temperature
T =
a /
2,
where is of
order unity and
depends somewhat on the frequency.
For general motions, hardly anything is known about the radiation. It is
clear that the effect must be a
nonlocal functional of the whole trajectory, because the relevant
wavelengths and
frequencies of the radiation may be of the order of scale lengths and
frequencies, respectively, that characterize the motion.
(For stationary motions, such as the two described above,
all points are equivalent, so the Unruh-like
radiation appears to depend only on "local" properties. However, the
non-local information on the stationarity of the
trajectory enters strongly.)
While the Unruh-like radiation may well serve as a marker for non-inertial motions it is still difficult to implicate it directly in the generation of inertia: 1. It is not clear that it carries all the information on the motion needed to produce inertia. For example, even for hyperbolic motion, can the direction of its acceleration be told by the accelerated observer (it should be remembered that the radiation is characterized by more than just its spectrum. For example, a finite size observer can compare the radiation in its different parts.) 2. If inertia is local-as it is to a very good approximation in the non-MOND regime-it has to adjust instantaneously to the state of motion. The latter may change however on time scales that are short compared with the typical period of the Unruh-like radiation. In the MOND regime there is no experimental indication that inertia is local; on the contrary, as mentioned before, theoretical arguments point to nonlocal MOND inertia.
How does MOND fit into this, and, in particular, how can the
connection with cosmology be made?
When the acceleration of a constant-a observer becomes smaller
than a0,
the typical frequency of its Unruh radiation becomes smaller than
the expansion
rate of the Universe, the Unruh wavelength becomes larger than
the Hubble distance, etc.
[30]
[3]. We expect then
some break in
the response
of the vacuum when we cross the a0 barrier. What is
the Unruh radiation
seen by a non-inertial observer in a nontrivial universe?
We know that even inertial observers
in a nontrivial universe find themselves immersed in radiation arising
from the distortion of the vacuum.
The simplest and best-studied case is that of a de Sitter
universe in which all
inertial observers see a thermal spectrum with a temperature
T
= ( /
3)1/3 /
2
[47],
where is the
cosmological constant characterizing the de Sitter cosmology.
It was shown in refs.
[48]
[49]
that an observer on an hyperbolic trajectory, in a de Sitter
universe, also sees thermal radiation, but with a temperature
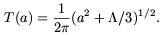
| (5) |
If inertia is what drives a non-inertial body back to (some nearby)
inertial state, striving to annul the vacuum radiation-here,
for hyperbolic motion, to drive T back to
T
- then T -
T
is a relevant quantity. (With cosmology fixed, the
best that inertia can do is drive T to
T;
in the cosmological context it also strives to drive
T
to zero.) We can write
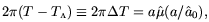
| (6) |
with
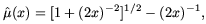
| (7) |
and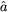 
0 =
2( / 3)1/2.
The quantity
T behaves in
just the manner required from MOND inertia
[1]
[
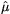(x
<< 1) x,
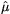(x
>> 1) 1 -
(2x)-1] with
a0 =
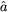0
naturally identified
with a cosmological acceleration parameter.
(This need not be the effective form of µ for trajectories
other than hyperbolic; in mondified inertia there is no µ
in the
theory itself, and a different form of µ may apply,
for instance, to circular orbits
[3]
[25].)
While this observation
is interesting and suggestive, I cannot tell whether it is germane
to MOND, because it is not backed by a concrete mechanism for inertia, and
because I cannot generalize the observation to more general motions.
In de Sitter space-time the expansion rate, the space-time curvature, and the cosmological constant are one and the same. These parameters differ from each other in a general Friedmanian universe, and so the above lesson learnt for the de Sitter case does not tell us which of the cosmological acceleration parameters is to be identified with a0 in the real universe.
Recall that, in MOND, inertia vanishes in the limit
a0
. In the above
picture this qualitative tenet of MOND is effected because the limit
corresponds to
, or H0
, etc.; so, the
Gibbons-Hawking-like radiation due to cosmology swamps the
thermal effects due to non-inertial motion: the
difference between inertial
and non-inertial observers is effaced in this limit.
Acknowledgments
I thank my friends Jacob Bekenstein and Bob Sanders for many helpful comments and discussions from which I have benefited over the years.