3. LIKELIHOOD RATIOS

Suppose it is known that either Hypothesis A or Hypothesis B must be true. And it is also known that if A is true the experimental distribution of the variable x must be f_A(x), and if B is true the distribution is f_B(x). For example, if Hypothesis A is that the K meson has spin zero, and hypothesis B that it has spin 1, then it is "known" that f_A(x) = 1 and f_B(x) = 2x, where x is the kinetic energy of the decay ^- divided by its maximum value for the decay mode K⁺ -> ^- + 2⁺.

If A is true, then the joint probability for getting a particular result of N events of values x₁, x₂,..., x_N is

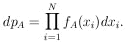
The likelihood ratio is

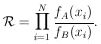
(1)

This is the probability, that the particular experimental result of N events turns out the way it did, assuming A is true, divided by the probability that the experiment turns out the way it did, assuming B is true. The foregoing lengthy sentence is a correct statement using direct probability. Physicists have a shorter way of saying it by using inverse probability. They say Eq. (1) is the betting odds of A against B. The formalism of inverse probability assigns inverse probabilities whose ratio is the likelihood ratio in the case in which there exist no prior probabilities favoring A or B. [3] All the remaining material in this report is based on this basic principle alone. The modifications applied when prior knowledge exists are discussed in Sec. 10.

An important job of a physicist planning new experiments is to estimate beforehand how many events he will need to "prove" a hypothesis. Suppose that for the K⁺ -> ^- + 2⁺ one wishes to establish betting odds of 10⁴ to 1 against spin 1. How many events will be needed for this? The problem and the general procedure involved are discussed in Appendix I: Prediction of Likelihood Ratios.