Annu. Rev. Astron. Astrophys. 1998. 36: 267-316 Copyright © 1998 by Annual Reviews. All rights reserved

3.2. The Proximity Effect: Measuring the Ionizing UV Background

The UV radiation from QSOs has been considered as the most natural origin for the ionization of the intergalactic gas (Arons & McCray 1969; Rees & Setti 1970). The finite number density of QSOs suggests that there may be inhomogeneities in the ionization state of the Ly clouds near each QSO. The term "Proximity Effect" (coined by Bajtlik et al 1988) refers to a relative lack of Ly absorption in the vicinity of the background QSO. The effect was first discussed by Weymann et al (1981), who also suggested the currently accepted explanation of increased ionization of the clouds by the nearby QSO. Carswell et al (1982) realized that the general increase of the absorption line density d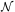 / dz with redshift was accompanied by a simultaneous decrease of d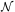 / dz in each individual QSO spectrum when approaching the QSO's emission redshift. Murdoch et al (1986) calling it the inverse effect confirmed and clarified this result. Tytler (1987b) referring to the effect as the anomaly, questioned the specific assumption that the reduced absorption is caused by the QSO's radiation field. Hunstead et al (1988), and Webb & Larsen (1987) defended the earlier interpretation, and in particular the claim that the effect is local to the neigborhood of the QSO.

If the proximity effect is indeed caused by enhanced ionization measuring the intensity of the ionizing UV background becomes possible from observations of the density of lines, d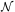 / dz, as a function of the distance from the QSO. Let us assume that in the vicinity of a QSO d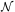 / dz is reduced, presumably owing to the excess ionization of the gas. With increasing distance from the emission redshift the QSO's ionizing flux decreases until the UV background intensity begins to dominate the ionization of the intergalactic gas. For example, at the point where the background intensity equals the QSO flux, L_Q(4 r_L²)^-1 (known from photometry), the neutral column density of a cloud should be lower by a factor of one half, with a corresponding decrease in d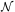 / dz for lines above a given detection threshold. In this way Carswell et al (1987) performed the first crude measurement of the UV background radiation field, obtaining J_-21 = 3, where J = J_-21 × 10^-21 erg cm^-2 s^-1 Hz^-1 sr^-1 is the intensity at the Lyman limit, 912 Å. Bajtlik et al (1988) confirmed this result from a larger low resolution sample of 19 QSOs, obtaining J_-21 = 1_-0.7^+3.2. Their measurement procedure (adopted by most later studies) consists of fitting the number density of lines per unit redshift distance X = 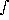(1 + z)dz

(9)

as a function of the luminosity distance r_L, where the background intensity J is the quantity desired. The quantity is again the exponent of the power law distribution of column densities. Lu et al (1991) with a larger sample get identical results. Bechtold (1994) in her even larger dataset finds J_-21 = 3. The largest compilations of high resolution data gave J_-21 = 0.5 ± 0.1 (Giallongo et al 1996), and J_-21 = 1^+0.5_-0.3 (Cooke et al 1997). None of these studies has found evidence for a significant change with redshift (for 1.6 < z < 4.1). However, Williger et al (1994) and Lu et al (1996) both found lower values (J_-21 = 0.2) just above z ~ 4, in contrast to Savaglio et al's (1997) value (J_-21 = 0.7) for the same redshift which is consistent with no evolution. In any case, when going to lower redshifts there appears to be a drastic decline in intensity below z ~ 1.6. At < z > ~ 0.5 Kulkarni & Fall (1993) obtained J_-21 = 6 × 10^-3 from HST FOS data (Bahcall et al 1993).

SYSTEMATIC EFFECTS ?     Assuming that the proximity effect really does measure the background intensity and not some other environmental effect caused by the QSO (e.g., suppression of neutral gas absorption in a high pressure environment) we still know this quantity only to within an order of magnitude, and the uncertainty may even be larger than that. This is because, in addition to the errors from line counting discussed in the previous section, there are systematic uncertainties in the QSO flux.

Espey (1993) has quantified the overestimate in the local QSO flux which arises from the well known systematic difference between the "actual" redshift of the QSO (as determined from narrow forbidden lines) and the redshift of the (usually blue-shifted) broad emission lines that define the "QSO redshift" used normally for the proximity effect. The blueshift may typically amount to ~ 1500 kms^-1. Downward corrections for J correspond to a factor of 2-3 in this case. These corrections have been taken account in the work by Williger et al (1994), Lu et al (1996), and Cooke et al (1997) but they would reduce for example the Bechtold value by a factor three.

Other uncertainties more difficult to quantify (see the review by Bechtold 1995) include QSO variability on the ionization time scale of the gas (Bajtlik et al 1988), gravitational lensing amplification of the apparent QSO luminosity, and uncertainties in the shape of the column density distribution (Chernomordik & Ozernoy 1993). Gravitational clustering of clouds near the QSOs may cause an excess number of clouds which again would lead to an overestimate of the background intensity by a factor up to three (Loeb & Eisenstein 1995).

The proximity effect measurements beg the question whether there are enough QSOs to produce the ionizing background seen, or whether an additional population of sources is needed. We may conclude as did Espey (see Espey 1993, and references therein) that the contribution of known QSOs to the background intensity agrees probably within the errors with the intensity from this measurement.

A related debate on whether the QSOs can ionize the IGM has occupied an even larger space in the literature. Unfortunately, we cannot do justice to this extended discussion here, but refer to some of the references in the section on the HeII Ly forest below.