Annu. Rev. Astron. Astrophys. 1998. 36: 267-316 Copyright © 1998 by Annual Reviews. All rights reserved

3.5. Spatial Structure along the Line of Sight: Clustering and Voids

Measurements of the two-point correlation function (TPCF) in velocity space along the LOS, (v), led Sargent et al (1980) to conclude that Ly clouds are not clustered as strongly as galaxies. Given the probability p of finding a pair of clouds with absorption cross section and space density n₀(z), separated by a velocity interval v, (v) is given by the following expression:

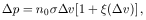
(13)

where v = cz / (1 + 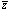) is the velocity splitting in the rest frame at mean redshift 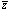. No correlation signal was found on scales of v between 300 and 30000 kms^-1. Clustering for small line pair splittings (v 300 kms^-1) would still be consistent with this result, given the limited resolution, and the effects of blending caused by the large line widths. Based on Voigt profiles fits to high resolution data Webb (1986) obtained the first evidence for the presence of a weak clustering signal ((100 kms^-1) 0.5, at z ~ 2.5) at small separations. This result has been confirmed by others (e.g., Muecket & Mueller 1987; Ostriker et al 1988). It is hard to detect the clustering at a high level of significance in any individual QSO spectrum because of the short redshift path length, and both detections and non-detections have been reported (Kulkarni et al 1996; Rauch et al 1992). A variety of techniques seem to indicate, however, that there really is weak clustering in the z ~ 3 forest on small scales. If Ly lines are considered as blends of components with intrinsically narrower line widths the clustering amplitude could be much higher (Rauch et al 1992). In particular, the strong clustering seen among metal absorption lines is largely invisible in Ly because of blending between the saturated Ly components associated with the metals. It is perhaps not that surprising that a Ly clustering amplitude, increasing with HI column density was actually reported (Chernomordik 1994; Cristiani et al 1995, 1997), and has been related to the clustering seen in metal absorption lines (Cowie et al 1995; Fernandez-Soto et al 1996). Earlier, Crotts (1989), by measuring the correlation in real space across the sky among systems in multiple LOS had reported an increase of clustering with Ly equivalent width.

STRUCTURE ON VARIOUS SCALES     The amplitude of the TPCF is not the only tool for measuring structure in the forest. In low resolution data, blends caused by clustering show up as a distortion in the equivalent width distribution of Ly lines, such that in the clustered case there are more large equivalent width lines and fewer small ones than for a random distribution of lines in velocity space (Barcons & Webb 1991). A number of other approaches, mostly equivalent to the hierarchy of correlation functions, or parts thereof (White 1979) may give a more robust clustering signal on small scales by including higher order correlations. Especially, the void probability function and, more generally, neighbor statistics ((Ostriker, Bajtlik & Duncan 1988; Liu & Jones 1990; Fang 1991; Meiksin & Bouchet 1995) have been used, invariably revealing the non-Poissonian (clustered) nature of the distribution of clouds in velocity space (Ostriker et al 1988; Bi et al 1989; Liu & Jones 1990; Babul 1991).

Structure has been detected on many different scales, in addition to the smale scale clustering described above: Fang (1991) used a Kolmogorov-Smirnov test for nearest neighbor intervals to detect a signal on scales 30-50 h^-1 Mpc (where h is the present day Hubble constant in units of 100 kms^-1Mpc^-1). Mo et al (1992), from an analysis of the extrema in the slope of the TPCF saw structure at 60 and 130 h^-1 Mpc. Meiksin & Bouchet (1995) found an anti-correlation in the TPCF around 3-6 h^-1 Mpc. Pando & Fang (1996), applying the wavelet transform, found clusters ~ 20 h^-1 Mpc in size in the Ly forest. The physical interpretation of the various results is not entirely obvious. The usefulness of the data for large scale structure analyses has always been accepted at face value, and it would certainly be entertaining to see whether there are systematic effects in the data, perhaps causing some of the structure. There are intrinsic scales in the spectra (like the quasi-periodic change in S/N ratio caused by the sensitivity maxima of the orders in an echelle spectrum) which are of similar magnitude (~ 5000 kms^-1, or ~ 25 h^-1 Mpc comoving at z ~ 3) as some of the above detections.

Most of the clustering work is based on analyzing correlations between distinct absorption lines. Including information about the relative strength of the absorption as a function of velocity splitting can improve the significance of any correlations, and give clues to the mechanism causing the signal. Webb & Barcons (1991) and Zuo (1992) have suggested correlating equivalent widths, rather than just lines above a detection threshold to search for inhomogeneities in the gas pressure or ionizing flux along the line of sight. Fardal & Shull (1993), Press et al (1993), and Zuo & Bond (1994) have extended this approach to statistical models of the pixel intensity correlations, a technique useful for disentangling line widths and small scale clustering on overlapping scales.

VOIDS IN THE FOREST     A specific discussion revolved around the question whether there are voids in the Ly forest, similar in comoving size to those seen in the local galaxy distribution. In principle verifying the existence of a void large enough to have a vanishing probability of occuring by chance, if drawn from a Poissonian distribution, is straightforward. The probability function for a Poissonian gap of size z in a spectrum with absorption line density d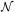 / dz is simply

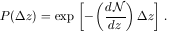
(14)

Carswell & Rees (1987) concluded that voids with sizes like those in the local universe (~ 50 h^-1 Mpc (comoving)) cannot fill more than 5% of the volume at < z > ~ 3.2. This result was confirmed by work by Duncan et al (1989), based on a larger dataset. A similar conclusion was reached by Pierre et al (1988), who found that the Ly absorbing gas cannot exhibit a void structure that is similar to that of low redshift galaxies, without producing strong clustering inconsistent with the observations.

Nevertheless, individual large gaps have been found. Crotts (1987), discovered an 43 h^-1 Mpc gap towards Q0420-388. This result was variously contested and confirmed in a dispute about significance levels (Ostriker et al 1988; Crotts 1989; Duncan et al 1989; Bi et al 1991, Rauch et al 1992), fuelled, among other things by the lack of a universally adopted definition of the term "void" which takes into account that a void may be void of lines only down to a certain detection threshold. It turned out that Crotts' gap, though not entirely empty, is a region of significantly lower line density. Dobrzycki & Bechtold (1991) found another void of size ~ 32 h^-1 Mpc in the spectrum of Q0302-003, and Cristiani et al (1995) discovered a significant pair of smaller voids towards Q0055-269. To summarize, the Ly forest does show the occasional gap, but the void structure apparent in the local galaxy population is not present in Ly absorbing gas.

The origin of the rare voids has most often been discussed in connection with a local proximity effect: A foreground QSO near the LOS to the more distant QSO produces a "clearing" by ionizing the adjacent clouds seen in the LOS to the other object (Bajtlik et al 1988; Kovner & Rees 1989). No clean-cut evidence has been found for this effect in the few studies done to date (Crotts 1989; Møller & Kjaergaard 1991), nor has it been possible to rule out its existence (e.g., for the 0302-003 void, see Dobrzycki & Bechtold 1991; Fernandez-Soto et al 1995). Several effects can complicate the analysis. Short of abandoning the idea of the proximity effect as an excess of ionization caused by a nearby QSO, anisotropic emission (beaming) by the QSO, and QSO variability can be invoked to explain the non-detections and the discrepancies between the redshift positions of QSO and candidate voids. The number of free parameters in such models is currently of the same order as the number of voids observed, suggesting that studies of individual voids will probably not be of great use for some time. With a sufficiently large dataset, global searches for fluctuations in the absorption pattern caused by an inhomogeneous radiation field (Zuo 1992; Fardal & Shull 1993) may have a better chance of success. However, Haardt & Madau (1996) have recently pointed out that the diffuse recombination radiation from Ly clouds themselves (which can provide on the order of 30% of the ionization rate) can considerably reduce the fluctuations.