


Many crucial events take place around the first seconds of the universe: a) the weak interaction decoupling at one MeV (one second or so); b) electron-positron annihilation around 0.5 MeV (four seconds or so); c) the nucleosynthesis of the light nuclides around 0.1 MeV (one hundred seconds or so). A useful approximation for the time temperature relationship is the following: t(sec) = 1/T2 (MeV).
As discussed before, at T > 1 MeV the weak interaction equilibrium is insured by the reactions:
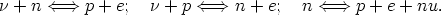
|
In consequence, the neutron-proton ratio is given by Boltzman law (fig 1):
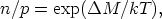
| (11) |
where  M is
the neutron-proton mass difference (1.293 MeV). As T
decreases, then/p ratio goes down from one to a value
close to 0.2 at
decoupling. After Td the neutrino capture reactions
are too slow to
compensate the neutron free desintegration
n
M is
the neutron-proton mass difference (1.293 MeV). As T
decreases, then/p ratio goes down from one to a value
close to 0.2 at
decoupling. After Td the neutrino capture reactions
are too slow to
compensate the neutron free desintegration
n 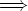 p + e +
p + e +  .
.
All through this period, the neutrons also have a nuclear
interaction with the protons, inducing the formation of a deuteron:
n + p
 D +
D +  .
.
The electron-positron annihilation at 0.5 MeV creates a flux of new
photons which increases slightly the photon radiation (more exactly
they slow down the cooling rate). Since the neutrino interactions are
now very weak, the neutrinos are essentially decoupled from the rest
of the universe and they receive no share of the energies released by
the annihilation. As a result the neutrino temperature
T becomes
slightly lower than the photon Tg.
becomes
slightly lower than the photon Tg.
This effect can be calculated through the conservation of entropy
per co-volume during the annihilation phase. The entropy density is
proportional to the number density of relativistic interacting
particles
s  g*T3. Here i and
f will stand for the initial state
(before annihilation) and the final state (after annihilation);
g*T3. Here i and
f will stand for the initial state
(before annihilation) and the final state (after annihilation);
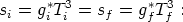
| (12) |
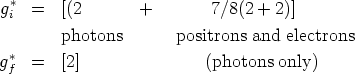
|
thus Tf / Ti = (11/4)1/3 = 1.31.
Since the neutrinos did not receive their share of this annihilation
phase they remained at Ti. Today we measure a photon
temperature
T of 2.7 K. Thus we expect that the neutrino radiation
is at T
of 2.7 K. Thus we expect that the neutrino radiation
is at T = 2
K. Such a cosmological background of neutrinos is a necessary prediction of
the theory if indeed the universe has reached temperatures over one
MeV in the past. Because of the low mean energy of these particles
(one MeV) its detection is outside of the realm of contemporary
technology.
= 2
K. Such a cosmological background of neutrinos is a necessary prediction of
the theory if indeed the universe has reached temperatures over one
MeV in the past. Because of the low mean energy of these particles
(one MeV) its detection is outside of the realm of contemporary
technology.
The previous example explains why various relativistic gases can be at different temperature as expressed in eq. (7) for g*. Suppose for instance that there exist right-handed neutrinos interacting as a weak interaction particle but with a coupling constant G' >> GF. If their decoupling temperature, evaluated through eq. (10), is larger than 107 MeV, the mass of the muon, they will receive no share from the muon annihilation at the equivalent temperature. Conservation of entropy during this phase, evaluated as in the previous example, will allow a determination of the temperature of this radiation, still lower today than the neutrino temperature.
Around 0.1 MeV the gamma rays (the tail of the Bose-Einstein photon
energy distribution) are no more numerous enough to keep the deuteron
D population in statistical equilibrium with the nucleons. This
is the onset of primordial nucleosynthesis. Through the reaction
n + p
 +
D, the population of D increases rapidly, as
shown in fig. 2. As they
reach a ratio of D/H of 10-3 or so, they
undergo further nuclear reactions and are transformed in mass-3 nuclei:
D + p
+
D, the population of D increases rapidly, as
shown in fig. 2. As they
reach a ratio of D/H of 10-3 or so, they
undergo further nuclear reactions and are transformed in mass-3 nuclei:
D + p
 3He +
3He +
 ;D +
n
;D +
n
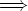 T +
T +
 . The
population of these mass-3 nuclei increases in turn as
the D fall down by many orders of magnitude.
. The
population of these mass-3 nuclei increases in turn as
the D fall down by many orders of magnitude.
The same fate happens to the mass-3 nuclei, as 4He
starts its rise through the
3He + 3He
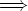 4He + 2p. Because there are
no stable nuclide
with mass 5 and 8, the 4He suffers essentially no
further nuclear
depletion. Only a very small fraction of its population gets
transformed in 7Li through
4He + T
4He + 2p. Because there are
no stable nuclide
with mass 5 and 8, the 4He suffers essentially no
further nuclear
depletion. Only a very small fraction of its population gets
transformed in 7Li through
4He + T
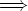
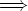 7Li +
7Li +
 and the
4He + 3He
and the
4He + 3He
 7Be +
7Be +
 ,
followed after many days by 7Be + e
,
followed after many days by 7Be + e
 7Li +
7Li +  . Some
7Li is further
destroyed but, because of its larger Coulomb charge (Z = 4), the
7Be
remains almost intact. This fact will play an important role in our
discussion of the quark-hadron transition.
. Some
7Li is further
destroyed but, because of its larger Coulomb charge (Z = 4), the
7Be
remains almost intact. This fact will play an important role in our
discussion of the quark-hadron transition.