5. UNDERLYING POPULATION AND PHOTON ESCAPE

5.1. Underlying absorption corrections to the emission line fluxes

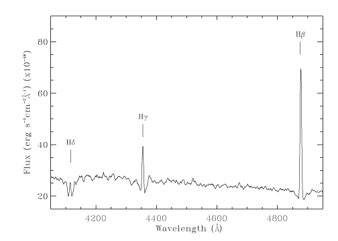
A clear signature of a population of young and intermediate age stars is the presence of the Balmer series in absorption in their optical spectrum. A complication is that in star forming objects, the Balmer emission lines from the ionized gas appear superimposed to the stellar absorption lines. This effect, growing in importance towards the higher order Balmer lines, is illustrated in Figure 3 where an example (NGC 1510) is shown. It can be seen that, while H emission is moderately affected by the absorption, all of the H emission is lost into the absorption. The equivalent width of the Balmer absorptions peaks at H - H and there is no detection of any absorption in H. This is due to the facts that the H absorption equivalent width is much smaller than that of H, and that the wings of the H absorption are difficult to detect due to the presence of forbidden [NII] doublet emission at 6548Å and 6584Å, right on top of both wings. In spectra of poorer S/N or lower spectral resolution than that of Figure 3, the wings of the Balmer absorptions are not detected and the result is an underestimate of the emitted fluxes and, more important for luminosity determinations, an overestimate of the internal extinction (Olofsson 1995).

Figure 3. A blue spectrum of the star forming galaxy NGC 1510 is shown to illustrate the effect of stellar Balmer absorptions in the measurement of the emission line strengths.

The observed ratio between two emission lines (e.g. H and H), when the underlying absorption is included, is:

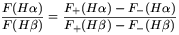
(6)

where F₊(H) and F₊(H) are the intrinsic emission line fluxes and F_-(H) and F_-(H) are the intrinsic fluxes of the corresponding absorption lines. This expression is correct in the case that the emission and the absorption lines have approximately equal widths.

Including the relation between the equivalent width, the flux of the continuum and the intensity of the line in equation 6 we obtain,

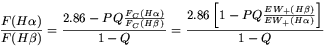
(7)

where, F_C(H) and F_C(H) are the continuum in H and H respectively, EW₊ and EW_- are the equivalent widths in emission and in absorption respectively for the different lines, Q = EW_-(H) / EW_+(H) is the ratio between the equivalent widths of H in absorption and in emission, P = EW_-(H) / EW_-(H) is the ratio between the equivalent widths in absorption of H and H and F₊(H) / F₊(H) = 2.86 is the theoretical ratio between H and H in emission for Case B recombination [Osterbrock 1989].

The value of P can be obtained from spectral evolutionary calculations like those of Olofsson (1995) For the case of solar abundance and stellar masses varying between 0.1 and 100 M within a Salpeter IMF, the value of P changes between 0.7 and 1 for ages between 1 and 15 million years respectively. This variation in the P parameter produces a change in the estimated F(H) / F(H) ratio of less than 2%, so in what follows we asssume P = 1.

For an instantaneous burst, the ratio EW_+(H) / EW_+(H) varies between 0.14 and 0.26 (Mayya 1995, Leitherer & Heckman 1995).

The corresponding equation for H and H is:

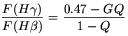
(8)

where G = EW_-(H) / EW_-(H) is the ratio between the equivalent widths in absorption of H and H and we assume for the respective emissions an intrinsic ratio of 0.47 for Case B recombination [Osterbrock 1989].

The evolution of the equivalent width of the Balmer absorption lines has been analyzed by González Delgado, Leitherer and Heckman (1999). In their models the parameter G is almost constant in time and independent of the adopted star formation history. We fixed the value of G to 1 as suggested by their results.

The effect of the underlying stellar absorptions is shown as a vector Q in Figure 4 (from equations 7 and 8). The whole time dependence is shown by the three closely grouped vectors. Its range is much smaller than typical observational errors. Dust extinction is also represented by a vector in the same plane (equation A8). It is possible, as these two vectors are not parallel, to solve simultaneously for underlying absorption (Q) and extinction (Av) for every object for which F(H), F(H) and F(H) are measured.

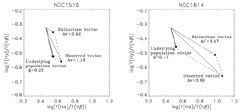
Figure 4. Logarithmic ratio of F(H) / F(H) vs. F(H) / F(H). The "observed vector" (from the intrinsic values given by recombination theory to the observed ratio) can be decomposed in two vectors, one is due to pure extinction and is given by Equation A8, the other one is given by Equations 7 and 8 and shows the effect of an underlying stellar population which is characterized by Q (see text). Plotted are the cases for NGC 1614 and NGC 1510. NGC 1614 is an example where the underlying absorption correction to the extinction estimate is not very large. NGC 1510 on the other hand, has a large correction.

We further illustrate the presence of underlying Balmer absorption in star forming galaxies in Figure 5 where we have plotted the galaxies from our sample in the log (F(H) / F(H)) vs. log (F(H) / F(H)) plane. Also shown are the vectors depicting dust extinction and the underlying absorption. Clearly, most observational points occupy the region below the reddening vector and to the right of the Balmer absorption vector. In the absence of underlying absorption all points should be distributed along the extinction vector. The fact that there is a clear spread below the extinction vector gives support to the underlying absorption scenario. We also find that the objects with smaller equivalent width of H are systematically further away from the pure extinction vector.

Figure 5. The galaxies from our sample are plotted in the Balmer decrement plane log (F(H) / F(H)) vs. log (F(H) / F(H)). The vectors indicate the direction of shifts due to extinction or underlying absorption from the intrinsic values given by recombination. The cross indicates typical 1 errors in the line ratios. Most points are, within the errors, below the reddening line and to the right of the underlying Balmer absorption line.

Four galaxies (NGC 3049, ESO 572, MRK 66 and NGC 1705) fall outside the space defined by the extinction and underlying absorption vectors, although two of them are within the errors. The other two (ESO 572 and MRK 66) are faint and reported as having been observed in less than optimum conditions in the original observations paper.

We have used this method to estimate simultaneously the "real" visual extinction Av ^* and the underlying Balmer absorption Q ^§. The values of Av ^* were then applied to the UV continuum and the emission line fluxes; the corrected values are listed in Table 2.

Table 2. Extinction properties, ultraviolet slope and photon escape probability of the galaxy sample. The second column is the extinction in magnitudes obtained with the MW extinction curve (see Appendix) without taking into account the effect of the underlying population. The third column is the extinction in magnitudes obtained by combining the MW extinction curve with the effect of an underlying population. The ratio between the equivalent widths of H in absorption and in emission as defined in Section 5.1 is given in the fourth column. Values of the ultraviolet slope (see appendix) are from Meurer et al. (1999) except for those marked with a where the values were extracted from Calzetti et al. (1994) and those marked with a where we calculated ourselves the parameter from the IUE data base spectra, following Calzetti et al. (1994) prescription. The escape probability is given in the sixth column (see text). Equivalent widths were calculated using Equation 1 except when marked with a * where they were taken from published spectroscopy.

Name	Av	Av *	Q × 100		(1 - )	EW(H)
NGC7673	1.84	1.11	27	-1.50	0.11	4.69
CAM0840	0.50	0.43	3	-1.26†	0.33	121*
CAM1543	0.67	0.67	0	-0.70†	-	224*
TOL1247	0.75	0.75	0	-0.47†	0.46	97*
NGC1313	3.06	2.45	23	-0.60‡	0.02	0.03
NGC1800	1.47	0.56	33	-1.65	0.56	1.10
ESO572	2.10	1.87	0	-1.96†	0.48	14.81
NGC7793	2.38	-	-	-1.34	0.04	0.06
UGCA410	0.97	0.37	23	-1.84	0.58	36.52
UGC9560	0.69	0.34	14	-2.02	0.51	36.63
NGC1510	1.19	0.62	22	-1.71	0.43	8.42
NGC1705	0.43	0.0	31	-2.42	0.81	4.20
NGC4194	2.91	2.73	8	-0.26	0.02	10.14
IC1586	2.02	1.37	25	-0.91	0.17	9.51
MRK66	0.00	0.00	23	-1.94	0.42	13.50
Haro15	0.73	0.27	18	-1.48	0.35	-
NGC1140	0.93	0.62	13	-1.78	0.34	11.19
NGC5253	0.32	0.12	9	-1.33	0.11	16.07
MRK542	1.66	-	-	-1.32	0.32	11.23
NGC6217	2.30	1.46	31	-0.74	0.05	1.30
NGC7714	1.65	1.57	4	-1.23	0.09	18.40
NGC1614	3.90	3.47	17	-0.76	0.01	5.82
NGC6052	1.33	0.98	14	-0.72	0.06	8.68
NGC5860	3.77	-	-	-0.91	0.12	4.02
NGC6090	1.80	1.62	8	-0.78‡	0.06	25.00
IC214	2.54	2.08	18	-0.61	0.05	3.14
MRK309	2.36	-	-	2.08†	0.03	3.68
NGC3049	1.21	1.01	0	-1.14	0.13	4.49
NGC4385	2.20	2.10	4	-1.02	0.09	6.60
NGC5236	1.44	0.56	32	-0.83	0.06	0.44
NGC7552	2.66	1.85	30	0.48	0.01	2.38

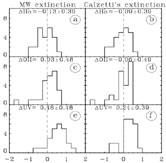
Figure 6 shows the result of taking into account the corrections for Balmer absorptions due to an underlying stellar population. The medians of both OII and H are close to zero indicating that including the underlying absorption correction brings into agreement the SFR in the optical with those in the FIR. At the same time UV shows still a positive value indicating an excess with respect to the FIR estimate. We must remember that while the ratio of emission line fluxes to FIR flux is not very sensitive to changes in the photon escape from object to object, this is not the case for the ratio of UV continuum to FIR fluxes. The reason being that while in the UV continuum we are detecting directly the escaped photons, i.e. those that do not heat the dust or ionize the gas, the emission lines and FIR fluxes are reprocessed radiation, i.e. the product of the radiation that does not escape the region.

Figure 6. The figure shows the histograms of the normalized SFR after the underlying stellar absorption effect is deducted from the extinction estimates, i.e. A*V is used instead of AV (Section 5.1). Panels a, c, e show the distributions after correcting the H, [OII]3727 and UV continuum using the MW extinction curve. b, d, and f show the result of using Calzetti's extinction curve. The median and standard deviation are given for each case. The total number of objects is 25.

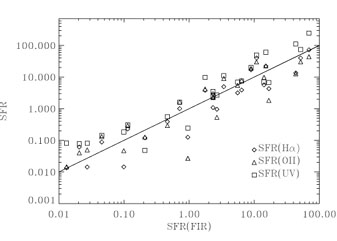
A striking aspect is the large reduction in the r.m.s. scatter in the UV from 0.70 before corrections to 0.39 after corrections, i.e. about half the original value. This simple fact suggests the goodness of the corrections applied to the data. This aspect is also illustrated in Figure 7 when compared to Figure 1.

Figure 7. Corrected SFR estimators vs. SFR(FIR). The corrections include the underlying Balmer absorption (see Section 5.1) and photon escape (see Section 5.2. The solid line represents equal values.

^§ See Appendix A for a detailed discussion on the dust extinction corrections to the observed fluxes. Back.