Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

2.4. The Volume V(r) in Robertson-Walker Spaces

One supposes that the space that describes any real universe must be homogeneous and isotropic. Otherwise, the notion of extension as applied to material bodies would have a complicated meaning. By this is meant that any material body, transported to any region of the space, must be transformed into itself without tearing or buckling. Such spaces are congruent. They can be rotated into themselves by a coordinate transformation without shear. This is not true for nonhomogeneous, non-isotropic spaces.

Robertson (1929, 1935) and Walker (1936) verified that the most general expression for the geometrical interval dl² between two points in a space of constant curvature with coordinates r,, , and r + dr, + d, and + d is

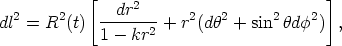
(7)

where k is the sign of the space curvature (+1 for k > 0, 0 for k = 0, -1 for k < 0). Various coordinate transformations give a variety of equivalent forms (e.g. McVittie 1956, 1965, Misner et al. 1973). Equation 7 is particularly convenient in deriving the various relations between the observable parameters and the geometry in the standard model.

The r, , numbers in Equation 7 are comoving coordinates. They are fixed (constant) for all time for a given galaxy. They are also dimensions. The factor R(t) is a scale factor (dimensions of length) that is a function of time in an expanding or contracting manifold. R(t) is independent of r, , and in a congruent space (one of constant curvature).

The volume enclosed within the space from the origin (r = 0, put at the observer) and the coordinate value r is

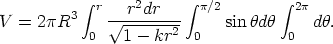
(8)

For k = 1 this integrates to

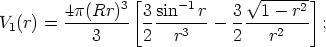
(9)

for k = - 1 to

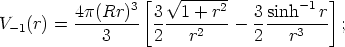
(10)

and for k = 0 to

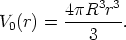
(11)

Note that r is not the interval distance from the origin to the point r, , . The manifold distance in the space described by Equation 7 is

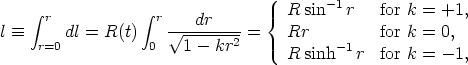
(12)

without loss of generality by rotating the coordinate system into the = = 0 plane. Hence, the coordinate r in Equations 9-11 is given in terms of the ratio of the measured distance l to the scale factor R (i.e. l /R), just as in Equations 2 and 4. (There should be no confusion about the changed definitions of l and r between Equations 2, 4, and 8-12). Explicitly,

(13)

Substituting Equation 13 into Equations 9, 10, and 11, and expanding for clarity to appreciate the dependence on the curvature, gives

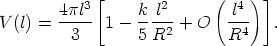
(14)

By analogy with Equations 2 and 4, kR^-2 is called the curvature of the space. Note that if k = 0, Equation 14 (i.e. Equation 11 also) gives the Euclidean volume.

The series expansion in Equation 14 illustrates the principle of the galaxy count-volume test. (In practice, of course, the exact equations are used.) If the distances l to a sample of galaxies were known and if a complete count of galaxies within this distance could be obtained, the curvature kR^-2 could be measured by the excess (or deficiency) of the counts from an l³ dependence. The distance l and hence the coordinate value of r (from Equation 13) are related to the redshift via the standard theory, to be developed in the next sections.