Copyright © 1988 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1988. 26:
561-630 Copyright © 1988 by Annual Reviews. All rights reserved |
6.1. Local Tests for Linearity of the Redshift-Distance Relation
6.1.1. THE PREDICTION If redshift is due to a real expansion of the geometrical manifold carrying the galaxies with it, the form of the velocity field must be isotropic and linear if space is isotropic and homogeneous. There are many ways to prove this. One of the most straightforward is to consider a triangle. If, upon expansion, the triangle is to be similar to itself, it follows directly that the velocity vi of any number of points along the sides of the triangle at distances ri from any arbitrary point must be
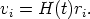
| (40) |
Otherwise the sides of the triangle will not expand with the same proportionality ratio. The factor H(t) sets the scale of the velocity field at time t.
A linear velocity field has two fundamental properties:
From these two properties it was early expected that the
velocity-distance relation for any reasonable model of an isotropic,
homogeneous universe (in the large) must be linear if redshift is a
true expansion of the manifold. Note also that the direct prediction
of the m(z) relation in the standard model (Equations 33
and 34), using m - M + 5 = 5 log r, gives cz
= H0r in the z
 0
limit, which
is Equation 40; this provides another way to prove that linearity is a
prediction of the standard model.
0
limit, which
is Equation 40; this provides another way to prove that linearity is a
prediction of the standard model.
6.1.2. THE DATA FOR SMALL z For light travel times that are small compared with the age of the Universe, the World picture is nearly the same as the World map, in Milne's (1935) useful language. The light travel time can be neglected for small-enough redshifts.
In the search for the form of the expansion law, the relevant redshift
regime in which to exploit this circumstance unencumbered by the
non-simultaneity of the observations is z
 0.2.
0.2.
Four claims are extant in the literature concerning the dependence of redshifts on distance in the World map. Only one of the following is correct.
 4000
km s-1); thereafter it becomes linear
(de Vaucouleurs 1958,
1972,
de Vaucouleurs & Peters
1986,
their Figures 2a, b;
Giraud 1985,
1986a,
b,
1987).
4000
km s-1); thereafter it becomes linear
(de Vaucouleurs 1958,
1972,
de Vaucouleurs & Peters
1986,
their Figures 2a, b;
Giraud 1985,
1986a,
b,
1987).
In his discovery paper, Hubble (1929) claimed a linear relation only quite locally, being aware of de Sitter's (1917) quadratic prediction [cf. Sandage (1975b) for a history]. Hubble's final sentence of this first paper was a cautious "and in this connection it may be emphasized that the linear relation found in the present discussion is a first approximation representing a restricted range in distance." His idea evidently was that he might only be observing a linear (tangent) approximation at very small r to the de Sitter v ~ r2 prediction, which might become evident at larger distances.
To test this, Humason (1931) began redshift measurements at Mount Wilson of bright E galaxies in clusters and found, even at this early date, values as large as cz ~ 20, 000 km s-1 for a cluster in Leo. With these new data, combined with estimates of apparent magnitude, Hubble & Humason (1931) extended the original Velocity-apparent magnitude relation approximately twentyfold in distance within two years of the initial discovery.
The slope of the redshift-magnitude relation was found to be 5 to within the errors, proving beyond doubt that the velocity-distance law is linear. However, in 1931 there were only 8 clusters involved in the test. By 1936, Hubble (1936a) and Humason (1936) had increased the data base to 10 clusters reaching cz = 42, 000 km s-1, with the same result. Hubble's (1953) last discussion, in his Darwin lecture, still had only 11 clusters, but the data now reached to z = 0.2, which was the largest redshift Humason could measure, even with the early use of the Palomar 200-inch reflector with photographic detection. The result again proved linearity, but the data sample was still small and the photometric measurements had been made using only photographic techniques. The final phase of the initial proof of linearity was the summary paper of HMS, which used new data on 18 clusters. However, the universality of the phenomenon was more inferred than established because there were still so few clusters.
Early claims of nonlinearity (cf. Hawkins 1962) used the HMS data on field galaxies taken from flux-limited samples and failed to correct for sample bias. Modern discussions of local nonlinearity, some of which are referenced earlier in this section, also use field galaxies. Because the luminosity function of field galaxies is considerably broader than for first-ranked cluster galaxies, some conclusions from these field galaxy studies have been criticized as due to insufficient corrections for the selection bias. Discussions of the bias have been given by Teerikorpi (1975a, b, 1984, 1987), Bottinelli et al. (1986, 1987, 1988), and Sandage (1988a, b). The principal consequences of bias neglect have been (a) an incorrectly high value of the Hubble constant and (b) a false belief that the consequent calculated variation of H0 with distance, increasing outward, is real (Section 9).
Discussion of the bias effects in the flux-limited RSA catalog became possible when the redshift coverage of that catalog became complete, following the finalization (Sandage 1978) of the Humason & Mayall (HMS) redshift program. The bias in the field galaxy sample was shown directly (Sandage et al. 1979), and the apparent increase of H0 with distance was demonstrated to be an artifact, caused by assigning a fixed <M> value to all galaxies in the flux-limited sample These selection effects are severe enough that study of the form of the redshift-distance relation using field galaxies is dangerous owing to the necessary corrections that are difficult to make accurately. For this reason, study of the m(z) relation to test for linearity was begun in the early 1970s using cluster and group samples. The photometry in these studies was done by photoelectric techniques; the results, reported in a series of papers (Sandage 1972a, b, c, 1973a, b, 1975a, 1986, Sandage et al. 1972, Sandage & Hardy 1973), again confirmed the linearity of the local velocity-distance relation.
The principal conclusion of the work was that the leading term of 5 log cz in the theoretical prediction of Equation 34 is fully confirmed. The standard model does, then, pass this most elementary of its predictions.