© CAMBRIDGE UNIVERSITY PRESS 2000

13.3. Rotating frame

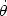It should be stressed that an orbit can appear open in one frame of reference and closed in another. In fact, suppose we move to a rotating frame for which the polar coordinates are (r, ), with = - _p; here _p is the angular velocity of the rotating frame. Then orbits are described by the new Hamiltonian ("Jacobi integral")

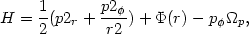(30)

with p = J, so that H = E - J _p. In the rotating frame, the important ratio 2 / becomes 2( - _p) / , which then may be rational or not depending on our choice of _p. In the dynamics of galaxies there are sometimes physical reasons that identify a specific value of the angular velocity of the rotating frame. The three important possible conditions of 2( - _p) / = -1, 0, +1 are often called condition of Inner Lindblad Resonance, Corotation, and Outer Lindblad Resonance, respectively (see Fig. 13.4). Thus, in the rotating frame, at the Lindblad resonances orbits appear closed into ellipses centered at r = 0. This feature, and the fact that - / 2 can be approximately constant on a wide radial range, led B. Lindblad to conjecture that two-armed spiral structure could persist as a kinematical wave in a differentially rotating disk (see Fig. 13.5).

Figure 13.4. Location of corotation and outer Lindblad resonance for a differentially rotating disk with respect to an assigned frequency p. The corotation circle divides the disk into two regions, one rotating faster ( < 0), the other rotating slower ( > 0) than p (after Bertin, G., Lin, C.C. 1996, Spiral Structure in Galaxies: A Density Wave Theory, MIT Press, Cambridge, MA, p. 79; © 1996 Massachusetts Institute of Technology).

Figure 13.5. Illustration of Lindblad's kinematic density waves (after Bertin, G., Lin, C.C. 1996, Spiral Structure in Galaxies: A Density Wave Theory, MIT Press, Cambridge, MA, p. 72; © 1996 Massachusetts Institute of Technology).