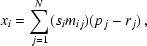2.1.2. Linear transformation matrix

The proposal to replace the CROTAi keywords of Wells et al. ([1981]) with a general linear transformation matrix dates from Hanisch & Wells ([1988]), although the details of its implementation have undergone considerable evolution. The main point of divergence has been whether the matrix should completely replace or simply augment the CDELTi, but there are also important differences relating to the default values of the matrix elements.

In defining a nomenclature which augments the CDELTi we have been guided by the following considerations:

• Where possible, standards should grow by generalizing existing usage rather than developing a separate parallel usage. Augmenting the existing CDELTi with a separate transformation matrix that defaults to unity makes old headers equivalent to new ones that omit the keywords that define the transformation matrix. In any case, the "once FITS, always FITS" rule means that FITS readers must continue to interpret CDELTi, so it makes sense for CDELTi to retain its original function.
• The transformation matrix then replaces the poorly defined CROTAi with a nomenclature that allows for both skew andfully general rotations. We do not consider this replacement and the consequent deprecation of the CROTAi to be inconsistent with the aim of generalizing existing usage since, to our knowledge, the CROTAi have had no formal definition other than the "AIPS convention" (Greisen [1983], [1986]). Both Wells et al. ([1981]) and Hanisch et al. ([2001]) state that "users of this option should provide extensive explanatory comments." Paper II describes the translation of the AIPS interpretation of CROTAi to the new formalism.
• A large fraction of WCS representations, perhaps the great majority, will not require the general linear transformation. FITS writers may continue to use CDELTi, so FITS-writing software need not be rewritten to conform to the new formalism unless it needs the new features.
• The physical units of a general image may differ by many orders of magnitude, from frequencies of 10¹⁰ Hz (or more) to angles of 10^-3 degrees (or less). If the physical units enter into the linear transformation matrix, then the elements of that matrix will have very different magnitudes. These issues pose difficulties both in computing and in understanding, and it may be simpler to defer application of physical units until the multiplication by CDELTi.
• These difficulties are compounded when correcting for the distortions present in real instruments. Paper IV will show that some instruments require distortion corrections before, and others after, the linear transformation matrix. Such corrections may need to be expressed in terms directly related to pixel coordinates. If the physical units enter into the linear transformation matrix, then the distortion corrections which come after the matrix would have to compensate for the physical units applied by it, effectively undoing and then redoing a multiplication by CDELTi. Furthermore, commensurability problems may arise when recording the maximum distortion correction for a WCS representation that mixes pre-, and post-corrections between axes.
• A widely used formalism that discards CDELTi was developed by the Space Telescope Science Institute for the Hubble Space Telescope and was incorporated generally in the IRAF data analysis system. We therefore support this as an alternative method.

In the PCi_j formalism, the matrix elements m_ij are encoded in

header cards, and s_i as CDELTi. The i and j indices are used without leading zeroes, e.g. PC1_1 and CDELT1. The default values for PCi_j are 1.0 for i = j and 0.0 otherwise. The PCi_j matrix must not be singular; it must have an inverse. Furthermore, all CDELTi must be non-zero. In other words, invertibility means that transformations which project from an initial coordinate system of dimensionality WCSAXES to a world coordinate system of dimensionality less than WCSAXES are forbidden.

In the CDi_j formalism Eqs. (1) and (2) are combined as

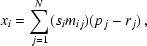(3)

and the

keywords encode the product s_im_ij. The i and j indices are used without leading zeroes, e.g. CD1_1. The CD i_j matrix must not be singular; it must have an inverse. CDELTi and CROTAi are allowed to coexist with CDi_j as an aid to old FITS interpreters, but are to be ignored by new readers. The default behavior for CDi_j differs from that for PCi_j; if one or more CDi_j cards are present then all unspecified CDi_j default to zero. If no CDi_j cards are present then the header is assumed to be in PCi_j form whether or not any PCi_j cards are present since this results in an interpretation of CDELTi consistent with Wells et al. ([1981]).

We specifically prohibit mixing of the PCi_j and CDi_j nomenclatures in any FITS header data unit. With this restriction, translation from the CDi_j formalism to the PCi_j formalism is effected simply in the keyword parsing stage of header interpretation; the CDi_j should be considered equivalent to the PCi_j subject to the considerations for default values noted above and with CDELTi set to unity. Similarly, CDi_j can be calculated from PCi_j and CDELTi following Eq. 3.