7.2. Relative Orientations of Angular Momenta

So far we have considered only the absolute values of orbital and internal angular momenta. It is no less important to know whether there is a systematic spatial orientation of spins with respect to one another and with respect to the orbital angular momentum of the pair. The data are still somewhat contradictory.

Kavraiskaia (1959) peformed a statistical analysis of the apparent shapes of double galaxies and concluded that there was a significant correlation in their angles of inclination from the line of sight. However, most of that sample are not in fact actual isolated pairs. Vorontsov-Vel'yaminov (1968) examined the direction of winding of spiral arms in 57 tight interacting pairs and found almost equal numbers (29:28) with the same or opposite directions of the spiral arms. However, according to Kogoshvili and Borchadze (1981), in double and multiple systems there is a statistically very significant excess of cases with different senses of the spiral arms in the components, i.e., counter-rotating galaxy spins.

Gorbachov (1970b) examined the apparent shapes of interacting and close pairs from the MCG catalogue and analysed the relative orientation of the galaxies. For the components of 1767 pairs he found a marked tendency to have the same angle of inclination with respect to the line of sight. In addition, from the distribution of the position angle of the major axis for 189 double galaxies, Gorbachov concluded that the sample exhibits an excess of coplanar double systems with 0. However, Gorbachov's analysis contained some errors, which were discussed by Noerdlinger (1979).

Arigo et al. (1978) measured the apparent shapes and position angles of 94 pairs from the Page and Turner samples. Analysing this subsample, Noerdlinger (1979) excluded any strong correlation in the planes of double galaxies but noted an excess number of pairs with the same position angle for the components. According to Sharp et al. (1979) the distribution of the position angle in 57 SS pairs from the Turner sample satisfies the expectation of a uniform random distribution. The same conclusion was reached earlier by Karachentsev and Fesenko (1975) using much richer observational material.

Conclusions about the relative orientations of spins for double spiral galaxies seen at an angle are based on the assumption of a consistent relationship between the direction of rotation of galaxies and the direction of curvature of their spiral arms. This assumption was examined by Pasha (1985). Among 190 galaxies for which the direction of rotation had been established almost all had trailing spiral arms and in only four cases did the arms appear to be leading. All four anomalous spirals are in double systems, three of which are found in our catalogue as numbers 295, 341 and 404. The unusual character of the spiral structures in these galaxies was accounted for by the tidal influence of the unusually close companions. However, note that one of these four anomalous cases of leading spiral arms was disproved by Sharp and Keel (1985), who studied NGC 5395 on large scale images taken at a 4-meter telescope.

Continuing the survey of observational data on spin orientations we examine two more works. Dickel et al. (1982) examined the relative direction of angular momenta in 10 pairs and found no evidence of any kind for any particular relative orientations. A different result was found by Helou (1984) who performed his own measurements as well as using the data of others. Measuring the relative angle ₁₂ between the spin vectors of galaxies in 22 pairs, Helou found a statistical effect of anticorrelation: 16 cases had ₁₂ > 90°, but not one had ₁₂ < 45°, i.e., spin directions close to one another. The spin orientations of these 22 pairs with respect to the projected orbital angular momentum showed a nearly random distribution.

As we have already remarked, the observed relative orientation of orbital and spin momenta is very relevant to the choice between various theories of galaxy formation.

Based on the formation of double galaxies from single compact objects with conservation of angular momentum, Ambartsumian (1958) proposed that in isolated pairs the spins should be oriented anti-parallel to one another. In a picture of primordial cosmological turbulence (Ozernoi, 1974), double or multiple systems are formed in primordial vortex cells and so the theory predicts parallel orientations of the spins and of the overall orbital momenta. In theories involving a tidal origin of the angular momentum of double galaxies (Peebles, 1969, Gott and Thuan, 1978) the spins should be preferentially oriented in the plane perpendicular to the line connecting their centers. As shown by the numerical experiments of Efstathiou and Jones (1979), however, the tidal mechanism cannot account for the observed magnitude of the angular momentum, of order K_G.

In recent years Chernin and his collaborators have proposed a new idea for the origin of the angular momenta of galaxies in multiple systems (Chernin, 1977, Ushakov and Chernin, 1983, Chernin and Ushakov, 1983, Chernin, 1987). A leading role is played by a mechanism involving irregular collisions of protogalactic gaseous fragments during the period of group formation. These random collisions will then generate protogalactic vorticity on large-scale shock fronts, and then the effects of dissipation will transfer angular momentum from the orbital motion of the fragments into the rotational motion of the protogalaxies. This scenario introduces a preferred relative orientation of orbital and spin momenta for pairs, with some preference for parallel spins.

These mechanisms for the origin of the angular momenta of galaxies and double systems have in common that the angular momentum must originate in the comparatively brief epoch of formation of the same galaxies. Various causes of a preferred orientation of the angular momenta in pairs have been recently examined by White. Modelling the interactions of two rotating galaxies and incorporating dynamical friction, White (1978, 1979) showed that the rate of this process depends on the spin orientations. The fastest merging takes place for galaxies for which the spins are oriented parallel to the orbital angular momentum. If the rotation of both components is opposite to the orbital rotation, then the merging is much slower. As a result of this coupled dynamical evolution there will be a deficit in the number of double galaxies for which all three momentum vectors are oriented in the same sense.

We now examine the observational material on the orientation of galaxies in the isolated pairs of the present catalogue. For each spiral galaxy we noted the direction of winding of the spiral arms on prints of the Palomar Atlas. The letter `s' indicates objects with the winding in the same sense as the letter, and the letter `z' indicates the opposite case, while galaxies for which it was not possible to determine the direction are indicated by `o'. In only 68 pairs could the direction of the spiral arms be determined for both components. Excluding false pairs with f > 100 the distribution by type of orientation is: 17 - sz, 20 - zs, 9 - ss, and 8 - zz ⁽¹³⁾ . We see that the number of pairs with parallel spins is significantly smaller than for the opposite case (17:37). The probability of getting this at random is p = 0.05 by ². Among 220 pairs for which the sense of winding of the spiral arms can be determined only for a single component, the distribution by type of orientation is 63 - so, 52 - os, 49 - zo, and 56 - oz, showing no significant asymmetry. It follows that subjective factors in determing the direction of spiral arms cannot be the cause of the observed excess in the number of double systems with opposed galaxy spins. From general considerations one might expect some kind of structural or dynamical difference between double galaxies with parallel or anti-parallel spins. However, a comparison shows that the differences between the two subsamples in structural type, apparent size, difference in magnitude, separation of components, orbital mass-to-luminosity ratio, or normalized moments µ₁₂, do not exceed those expected from chance fluctuations. To improve these statistics it is important to examine the spiral structure on large scale images.

Another possibility is based on spectral observations. For this approach we select isolated pairs satisfying the following criteria: both components of the system have emission spectra with significant inclination of the spectral lines from rotation, nearly the same position angle for the major axis of both galaxies ( < 30°), and both galaxies well inclined to the line of sight (apparent shape e₁, e₂ < 0.5). This last selection minimizes the uncertainty in the spatial orientation of spins because the disk of the galaxy (along its major axis) is nearly in the direction of observation. Among 19 double systems satisfying these selection criteria, cases with the same and opposite senses of spin are almost equal (9:10).

We further examined close pairs for which the spectrograph slit was oriented between the centers of both components. Limitations on the position angle and apparent shapes of the galaxies were as established previously. In this case we can determine the direction of the spins with respect to one another and also with respect to the projected orbital angular momentum. The orientation possibilities of the three rotation vectors, along with the appearance of the emission lines on the spectrogram, are shown in figure 51. The dashed lines indicate the spectrograph slit located between the centers of galaxies and the filled lines indicate the appearance of spectral lines. The large and small vectors indicate the rotation vectors of the brighter and fainter components and the double-line vector indicates the direction of orbital rotation. For a random orientation of angular momenta all four combinations, A, B, C, and D should be equally common. The observed numbers are: 7 - A, 5 - B, 8 - C, and 7 - D. These data do not suggest any particular relation between the orbital and angular momenta of double galaxies.

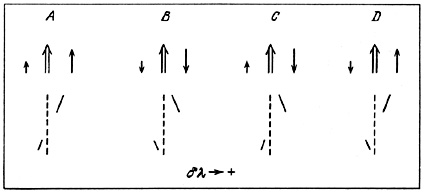Figure 51.

Karachentsev and Mineva (1984b) examined the statistics of spin orbit configurations in galaxy pairs. Figures 52 and 53 show reproductions of 18 double systems taken from the blue charts of the Palomar Atlas. Each field covers 9' × 6' with north up and east to the left, and the numbers are according to the Karachentsev (1972) catalogue. We determined the direction of rotation of each component from spectral observations. For each galaxy the receding side is indicated by a `+' sign and the approaching side by a `-' sign. Similarly, from the radial velocities we have indicated the approaching and receding components with respect to the center of each pair. As in the two previous spectrally observed subsamples, here as well we find no evidence for any ordering of the orientation of spins: 10 cases have parallel spins and orbits, while for 8 cases the galaxy is rotating in the other direction. Because of projection effects a reliable determination of the spin orientation with respect to the orbital motion is possible for only a small number of objects. The assumption of a uniform random distribution of spin orientations for the brighter and fainter components with respect to the orbital momentum is not contradicted by the present limited observational data.

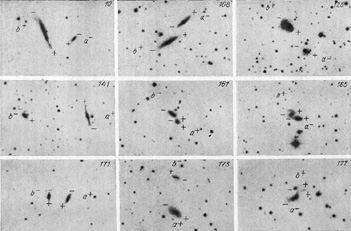Figure 52.

We note that Helou (1984) did not find a single example in his 22 pairs with the angle between spin vector components ₁₂ < 45°. From the above subsample (see figures 52 and 53) we see three examples (numbers 108, 171 and 430) which have ₁₂ < 45° and thus cause the `downfall' of Helou.

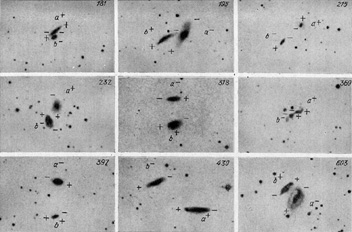Figure 53.

Any relative ordering of spins should lead to a correlation of apparent shapes and a non-random relative orientation of the major axes of pair components. This was tested by Karachentsev and Fesenko (1975), but gave rather uncertain results. Figure 54 shows the distribution of 339 spiral-spiral pairs according to the apparent shapes of the brighter (e₁) and fainter (e₂) components. Non-isolated pairs with f > 100 were excluded. The (e₁, e₂) distribution for spiral galaxies shows a slight correlation with coefficient +0.13 ± 0.09. This weak effect reflects not a correlation in the angles of inclination (i = cos^-1e) but the correlation of double galaxies by structural type and true shape. This is easy to show from the distribution of (e₁, e₂) split up into pairs with the same morphological type (SaSa, ..., SmSm).

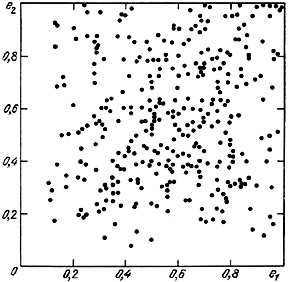Figure 54.

The distribution of 190 isolated SS pairs by position angles of the brighter (₁) and fainter (₂) members is shown in figure 55. The position angles of the major axis of the galaxies were measured with respect to the line connecting their centers. Neither the primary components nor the satellites show evidence of any preferred alignment of the major axis. By a ² criterion the diagram is very well represented by a uniform random distribution. We note that the data in figure 55 represent very strict limits on the relative fraction of pairs in the catalogue with colinear spins. Thus, an excess of as little as 20% of nearly coplanar double systems, (|₁ - ₂| < 30°) would produce a diagonalizing effect over and above the Poisson picture with significance in excess of 5. Thus the sort of anisotropies reported by Kogoshvili and Borchadze (1981) and Helou (1984) still require further observational tests.

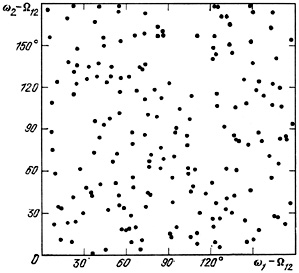Figure 55.

The random orientation of the disks in double galaxies may be due to their mutual tidal influence. In tight pairs the effects of precession and nutation should be important. An approximate expression for the precession period T_pr is:

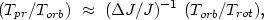(7.10)

where T_orb is the orbital period of the pair, T_rot is the internal rotation period of the galaxy, and (J / J) is the relative difference of the moments of inertia of the galaxy along the major and minor axes. For contact pairs consisting of spiral galaxies both of the above dimensionless ratios differ only slightly from unity. Therefore the precession period for the majority of double galaxies has a value ~ 10⁹ years, considerably smaller than their cosmological ages H^-1 10¹⁰ years.

Obviously, precession and nutation are weak for double elliptical galaxies with only small internal rotation. This may explain the fact that the correlation of apparent shapes (orientations) is much stronger for EE pairs than for systems with spiral components.

Finally, the process ordering the spins of double galaxies is probably most active during early cosmological epochs when the dimensions of protogalaxies were comparable to the separations of double systems. A leading role might have been played by the dissipation of mass and angular momentum during the non-stationary formation of protosystems.

---

¹³ As usual, the first symbol indicates the western component of a pair. Back.