The basic picture of Big Bang cosmology, a hot, uniform early universe
expanding
and cooling at late times, is very successful and has (so far) passed a
battery of
increasingly precise tests. It successfully explains the observed
primordial
abundances of elements, the observed redshifts of distant galaxies, and
the presence
of the cosmic microwave background. Observation of the CMB is a field
that is currently
progressing rapidly, allowing for extremely precise tests of
cosmological models. The
most striking feature of the CMB is its high degree of uniformity, with
inhomogeneities
of about one part in 105. Recent precision measurements of
the tiny anisotropies in
the CMB have allowed for constraints on a variety of cosmological
parameters. Perhaps
most importantly, observations of the first acoustic peak, first
accomplished with precision by the Boomerang
[23] and MAXIMA
[24]
experiments, indicate that the geometry of the universe is flat, with
total =
1.02 ± 0.05
[22].
However, this success of the
standard Big Bang leaves us with a number of vexing puzzles. In
particular, how did the universe get so big, so flat, and so uniform? We
shall see that these observed characteristics of the universe are poorly
explained by the standard Big Bang scenario, and we will need to add
something to the standard picture to make it all make sense: inflation.
We observe that the universe has a nearly flat geometry,
tot
1.
However, this is far from a natural expectation for an arbitrary FRW
space. It is simple to see why. Take the defining expression for
,
 |
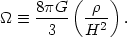(59) |
Here the density of matter with equation of state
p =
w
evolves with expansion as
 |
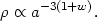(60) |
Using this and the Friedmann equation (12) it is possible to derive a
simple expression for how
evolves with expansion:
 |
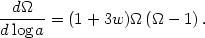(61) |
This is most curious! Note the sign. For an equation of state with 1 + 3w > 0, which is the case for any kind of "ordinary" matter, a flat universe is an unstable equilibrium:
 |
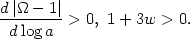(62) |
So if the universe at early times deviates even slightly from a flat
geometry, that deviation will grow large at late times. If the universe
today is flat to within
1 ± 0.05, then
the time of
recombination was
= 1 ± 0.00004,
and at nucleosynthesis
= 1 ±
10-12. This leaves unexplained how the universe
got so perfectly flat in the first place. This curious fine-tuning in
cosmology is referred to as the flatness problem.