4.6. The primordial power spectrum

Summarizing the results of the last section, inflation predicts not only a flat, smooth universe, but also provides a natural mechanism for the production of primordial density and gravitational wave fluctuations. The scalar, or density fluctuation amplitude when a mode crosses the horizon is given by

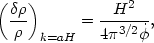(102)

and the gravitational wave amplitude is given by

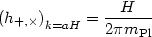(103)

for each of the two polarization modes for the gravitational wave. These are the amplitudes for a single mode when its wavelength (which is changing with time due to expansion) is equal to the horizon size. In the case of slow roll, with 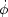small and H slowly varying, modes of different wavelengths will have approximately the same amplitudes, with slow variation as a function of scale. If we define the power spectrum as the variance per logarithmic interval,

(104)

inflation generically predicts a power-law form for P_S(k),

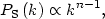(105)

so that the scale invariant spectrum, one with equal amplitudes at horizon crossing, is given by n = 1. The current observational best fit for the spectral index n is [32]

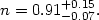(106)

The observations are in agreement with inflation's prediction of a nearly (but not exactly) scale-invariant power spectrum, corresponding to a slowly rolling inflaton field and a slowly varying Hubble parameter during inflation. One can also consider power spectra which deviate from a power law,

(107)

but inflation predicts the variation in the spectral index dn / d logk to be small, and we will not consider it further here. Similarly, the tensor fluctuation spectrum in inflationary models is a power-law,

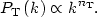(108)

(Note the unfortunate convention that the scalar spectrum is defined as a power law with index n - 1 while the tensor spectrum is defined as a power law with index n_T, so that the scale-invariant limit for tensors is n_T = 0!)

It would appear, then, that we have four independent observable quantities to work with: the amplitudes of the scalar and tensor power spectra at some fiducial scale k_*:

(109)

and the spectral indices n,n_T of the power spectra. (Generally, the scale k_* is taken to be about the scale of the horizon size today, corresponding to the CMB quadrupole.) In fact, at least within the context of inflation driven by a single scalar field, not all of these parameters are independent. This is because the tensor spectral index is just given by the equation of state parameter ,

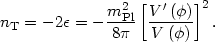(110)

However, from Eqs. (102) and (103), and from the equation of motion in the slow-roll approximation (86), we have a simple expression for the ratio between the amplitudes of tensor and scalar fluctuations:

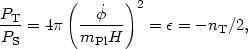(111)

so that the tensor/scalar ratio and the tensor spectral index are not independent parameters, but are both determined by the equation of state during inflation, a relation known as the consistency condition for slow-roll inflation. ⁽¹⁰⁾ It is conventional to define the tensor scalar ratio as the ratio r of the contributions of the modes to the CMB quadrupole, which adds roughly a factor of 10 [33]:

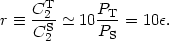(112)

Similarly, the scalar spectral index can be expressed in terms of a second slow roll parameter ,

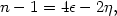(113)

where depends on the second derivative of the potential,

(114)

So any simple inflation model gives us three independent parameters to describe the primordial power spectrum: the amplitude of scalar fluctuations A_S, the tensor/scalar ratio r, and the scalar spectral index n. The important point is that these are observable parameters, and will allow us to make contact between the physics of very high energies and the world of observational cosmology, in particular the cosmic microwave background. In the next section, we will see in detail how to accomplish this for a simple model.

¹⁰ In the case of multi-field inflation, this condition relaxes to an inequality, P_T / P_S - 2n_T [34]. Back.