10.1. The connection between thermodynamics and spacetime geometry

The existence of one-way membranes, however, is not necessarily a feature of gravity or curved spacetime and can be induced even in flat Minkowski spacetime. It is possible to introduce coordinate charts in Minkowski spacetime such that regions are separated by horizons, a familiar example being the coordinate system used by a uniformly accelerated frame (Rindler frame) which has a non-compact horizon. The natural coordinate system (t, x, y, z) used by an observer moving with a uniform acceleration g along the x-axis is related to the inertial coordinates (T, X, Y, Z) by

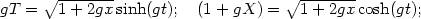(157)

and Y = y;Z = z. The metric in the accelerated frame will be

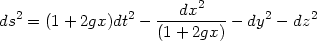(158)

which has the same form as the metric in (153) with f (x) = (1 + 2gx). This has a horizon at x = - 1/2g with the surface gravity = g and temperature T = (g / 2). All the horizons are implicitly defined with respect to certain class of observers; for example, a suicidal observer plunging into the Schwarzschild black hole will describe the physics very differently from an observer at infinity. From this point of view, which we shall adopt, there is no need to distinguish between observer dependent and observer independent horizons. This allows a powerful way of describing the thermodynamical behaviour of all these spacetimes (Schwarzschild, de Sitter, Rindler ....) at one go.

The Schwarzschild, de Sitter and Rindler metrics are symmetric under time reversal and there exists a `natural' definition of a time symmetric vacuum state in all these cases. Such a vacuum state will appear to be described a thermal density matrix in a subregion of spacetime with the horizon as a boundary. The QFT based on such a state will be manifestedly time symmetric and will describe an isolated system in thermal equilibrium in the subregion . No time asymmetric phenomena like evaporation, outgoing radiation, irreversible changes etc can take place in this situation. We shall now describe how this arises.

Consider a (D+1) dimensional flat Lorentzian manifold with the signature (+, - , - ,...) and Cartesian coordinates Z^A where A = (0, 1, 2,..., D). A four dimensional sub-manifold in this (D+1) dimensional space can be defined through a mapping Z^A = Z^A(x^a) where x^a with a = (0, 1, 2, 3) are the four dimensional coordinates on the surface. The flat Lorentzian metric in the (D+1) dimensional space induces a metric g_ab(x^a) on the four dimensional space which - for a wide variety of the mappings Z^A = Z^A(x^a) - will have the signature (+ , - , - , -) and will represent, in general, a curved four geometry. The quantum theory of a free scalar field in is well defined in terms of the, say, plane wave modes which satisfy the wave equation in . A subset of these modes, which does not depend on the `transverse' directions, will satisfy the corresponding wave equation in and will depend only on x^a. These modes induce a natural QFT in . We are interested in the mappings Z^A = Z^A(x^a) which leads to a horizon in so that we can investigate the QFT in spacetimes with horizons using the free, flat spacetime, QFT in ([294] [289]).

For this purpose, let us restrict attention to a class of surfaces defined by the mappings Z^A = Z^A(x^a) which ensures the following properties for : (i) The induced metric g_ab has the signature (+ , - , - , -). (ii) The induced metric is static in the sense that g₀ = 0 and all g_abs are independent of x⁰. [The Greek indices run over 1,2,3.] (iii) Under the transformation x⁰ x⁰ ± i(/g), where g is a non zero, positive constant, the mapping of the coordinates changes as Z⁰ - Z⁰, Z¹ - Z¹ and Z^A Z^A for A = 2,..., D. It will turn out that the four dimensional manifolds defined by such mappings possess a horizon and most of the interesting features of the thermodynamics related to the horizon can be obtained from the above characterization. Let us first determine the nature of the mapping Z^A = Z^A(x^a) = Z^A(t,x) such that the above conditions are satisfied.

The condition (iii) above singles out the spatial coordinate Z¹ from the others. To satisfy this condition we can take the mapping Z^A = Z^A(t, r, , ) to be of the form Z⁰ = Z⁰(t, r), Z¹ = Z¹(t, r), Z = Z(r, , ) where Z denotes the transverse coordinates Z^A with A = (2,..., D). To impose the condition (ii) above, one can make use of the fact that possesses invariance under translations, rotations and Lorentz boosts, which are characterized by the existence of a set of N = (1/2)(D + 1)(D + 2) Killing vector fields _A(Z^A). Consider any linear combination V^A of these Killing vector fields which is time like in a region of . The integral curves to this vector field V^A will define time like curves in . If one treats these curves as the trajectories of a hypothetical observer, then one can set up the proper Fermi-Walker transported coordinate system for this observer. Since the four velocity of the observer is along the Killing vector field, it is obvious that the metric in this coordinate system will be static [295]. In particular, there exists a Killing vector which corresponds to Lorentz boosts along the Z¹ direction that can be interpreted as rotation in imaginary time coordinate allowing a natural realization of (iii) above. Using the property of Lorentz boosts, it is easy to see that the transformations of the form Z⁰ = lf (r)^1/2sinh gt;Z¹ = ± lf (r)^1/2cosh gt will satisfy both conditions (ii) and (iii) where (l, g) are constants introduced for dimensional reasons and f (r) is a given function. This map covers only the two quadrants with | Z¹| > | Z⁰| with positive sign for the right quadrant and negative sign for the left. To cover the entire (Z⁰, Z¹) plane, we will use the full set

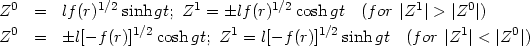(159)

The inverse transformations corresponding to (159) are

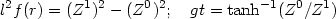(160)

Clearly, to cover the entire two dimensional plane of - < (Z⁰, Z¹) < + , it is necessary to have both f (r) > 0 and f (r) < 0. The pair of points (Z⁰, Z¹) and (- Z⁰, - Z¹) are mapped to the same (t, r) making this a 2-to-1 mapping. The null surface Z⁰ = ± Z¹ is mapped to the surface f (r) = 0.

The transformations given above with any arbitrary mapping for the transverse coordinate Z = Z(r, , ) will give rise to an induced metric on of the form

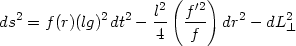(161)

where dL² depends on the form of the mapping Z = Z(r, , ). This form of the metric is valid in all the quadrants even though we will continue to work in the right quadrant and will comment on the behaviour in other quadrants only when necessary. It is obvious that the , in general, is curved and has a horizon at f (r) = 0.

As a specific example, let us consider the case of (D + 1) = 6 with the coordinates (Z⁰, Z¹, Z², Z³, Z⁴, Z⁵) = (Z⁰, Z¹, Z², R, , ) and consider a mapping to 4-dimensional subspace in which: (i) The (Z⁰, Z¹) are mapped to (t, r) as before; (ii) the spherical coordinates (R,, ) in are mapped to standard spherical polar coordinates in : (r,, ) and (iii) we take Z² to be an arbitrary function of r: Z² = q(r). This leads to the metric

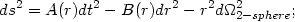(162)

with

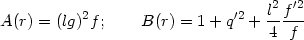(163)

Equation (162) is the form of a general, spherically symmetric, static metric in 4-dimension with two arbitrary functions f (r), q(r). Given any specific metric with A(r) and B(r), equations (163) can be solved to determine f (r), q(r). As an example, let us consider the Schwarzschild solution for which we will take f = 4(1 - (l / r)); the condition g₀₀ = (1 / g₁₁) now determines q(r) through the equation

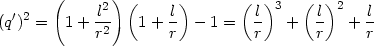(164)

That is

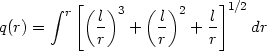(165)

Though the integral cannot be expressed in terms of elementary functions, it is obvious that q(r) is well behaved everywhere including at r = l. The transformations (Z⁰, Z¹) (t, r);Z² q(r); (Z³, Z⁴, Z⁵) (r, , ) thus provide the embedding of Schwarzschild metric in a 6-dimensional space. [This result was originally obtained by Frondsal [296]; but the derivation in that paper is somewhat obscure and does not bring out the generality of the situation]. As a corollary, we may note that this procedure leads to a spherically symmetric Schwarzschild-like metric in arbitrary dimension, with the 2-sphere in (162) replaced any N-sphere.

The choice lg = 1, f (r) = [1 - (r / l)²] will provide an embedding of the de Sitter spacetime in 6-dimensional space with Z² = r, (Z³, Z⁴, Z⁵) (r, , ). Of course, in this case, one of the coordinates is actually redundant and - as we have seen earlier - one can achieve the embedding in a 5-dimensional space. A still more trivial case is that of Rindler metric which can be obtained with D=3, lg = 1, f (r) = 1 + 2gr; in this case, the "embedding" is just a reparametrization within four dimensional spacetime and - in this case - r runs in the range (- , ). The key point is that the metric in (161) is fairly generic and can describe a host of spacetimes with horizons located at f = 0. We shall discuss several features related to the thermodynamics of the horizon in the next few sections.