10.4. Conceptual issues in de Sitter thermodynamics

The analysis in the last few sections was based on a strictly static 4-dimensional spacetime. The black hole metric, for example, corresponds to an eternal black hole and the vacuum state which we constructed in section 10.2 corresponds to the Hartle-Hawking vacuum [317] of the Schwarzschild spacetime, describing a black hole in thermal equilibrium. There is no net radiation flowing to infinity and the entropy and temperature obtained in the previous sections were based on equilibrium considerations.

As we said before, there are two different ways of defining the entropy. In statistical mechanics, the entropy S(E) is related to the degrees of freedom [or phase volume] g(E) by S(E) = ln g(E). Maximization of the phase volume for systems which can exchange energy will then lead to equality of the quantity T(E) ( S / E)^-1 for the systems. It is usual to identify this variable as the thermodynamic temperature. The analysis of BH temperature based on Hartle-Hawking state is analogous to this approach.

In classical thermodynamics, on the other hand, it is the change in the entropy which can be operationally defined via dS = dE/T(E). Integrating this equation will lead to the function S(E) except for an additive constant which needs to be determined from additional considerations. This suggests an alternative point of view regarding thermodynamics of horizons. The Schwarzschild metric, for example, can be thought of as an asymptotic limit of a metric arising from the collapse of a body forming a black-hole. While developing the QFT in such a spacetime containing a collapsing black-hole, we need not maintain time reversal invariance for the vacuum state and - in fact - it is more natural to choose a state with purely in-going modes at early times like the Unruh vacuum state [318]. The study of QFT in such a spacetime shows that, at late times, there will exist an outgoing thermal radiation of particles which is totally independent of the details of the collapse. The temperature in this case will be T(M) = 1/8 M, which is the same as the one found in the case of the state of thermal equilibrium around an "eternal" black-hole. In the Schwarzschild spacetime, which is asymptotically flat, it is also possible to associate an energy E = M with the black-hole. Though the calculation was done in a metric with a fixed value of energy E = M, it seems reasonable to assume that - as the energy flows to infinity at late times - the mass of the black hole will decrease. If we make this assumption - that the evaporation of black hole will lead to a decrease of M - then one can integrate the equation dS = dM / T(M) to obtain the entropy of the black-hole to be S = 4 M² = (1/4)(A / L_P²) where A = 4(2M)² is the area of the event horizon and L_P = (G 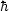/ c³)^1/2 is the Planck length. ⁽²⁾ The procedure outlined above is similar in spirit to the approach of classical thermodynamics rather than statistical mechanics.

Once it is realized that only the asymptotic form of the metric matters, we can simplify the above analysis by just choosing a time asymmetric vacuum and working with the asymptotic form of the metric with the understanding that the asymptotic form arose due to a time asymmetric process (like gravitational collapse). In the case of black hole spacetimes this is accomplished - for example - by choosing the Unruh vacuum [318]. The question arises as to how our unified approach fares in handling such a situation which is not time symmetric and the horizon forms only asymptotically as t .

There exist analogues for the collapsing black-hole in the case of de Sitter (and even Rindler) [293]. The analogue in the case of de Sitter spacetime will be an FRW universe which behaves like a de Sitter universe only at late times [like in equation (27); this is indeed the metric describing our universe if = 0.7, _NR = 0.3]. Mathematically, we only need to take a(t) to be a function which has the asymptotic form exp(Ht) at late times. Such a spacetime is, in general, time asymmetric and one can choose a vacuum state at early times in such a way that a thermal spectrum of particles exists at late times. Emboldened by the analogy with black-hole spacetimes, one can also directly construct quantum states (similar to Unruh vacuum of black-hole spacetimes) which are time asymmetric, even in the exact de Sitter spacetime, with the understanding that the de Sitter universe came about at late times through a time asymmetric evolution.

The analogy also works for Rindler spacetime. The coordinate system for an observer with time dependent acceleration will generalize the standard Rindler spacetime in a time dependent manner. In particular, one can have an observer who was inertial (or at rest) at early times and is uniformly accelerating at late times. In this case an event horizon forms at late times exactly in analogy with a collapsing black-hole. It is now possible to choose quantum states which are analogous to the Unruh vacuum - which will correspond to an inertial vacuum state at early times and will appear as a thermal state at late times. The study of different `vacuum' states shows [293] that radiative flux exists in the quantum states which are time asymmetric analogues of the Unruh vacuum state.

A formal analysis of this problem will involve setting up the in and out vacua of the theory, evolving the modes from t = - to t = + , and computing the Bogoliubov coefficients. It is, however, not necessary to perform the details of such an analysis because all the three spacetimes (Schwarzschild, de Sitter and Rindler) have virtually identical kinematical structure. In the case of Schwarzschild metric, it is well known that the thermal spectrum at late times arises because the modes which reach spatial infinity at late times propagate from near the event horizon at early times and undergo exponential redshift. The corresponding result occurs in all the three spacetimes (and a host of other spacetimes).

Consider the propagation of a wave packet centered around a radial null ray in a spherically symmetric (or Rindler) spacetime which has the form in equation (162) or (175). The trajectory of the null ray which goes from the initial position r_in at t_in to a final position r at t is determined by the equation

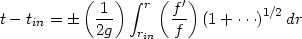(186)

where the ^... denotes terms arising from the transverse part containing dr² (if any). Consider now a ray which was close to the horizon initially so that (r_in - l ) << l and propagates to a region far away from the horizon at late times. (In a black hole metric r >> r_in and the propagation will be outward directed; in the de Sitter metric we will have r << r_in with rays propagating towards the origin. ) Since we have f (r) 0 as r l, the integral will be dominated by a logarithmic singularity near the horizon and the regular term denoted by ^... will not contribute. [This can be verified directly from (162) or (175).] Then we get

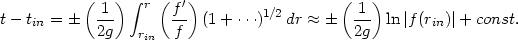(187)

As the wave propagates away from the horizon its frequency will be red-shifted by the factor (1 / (g₀₀)^1/2) so that

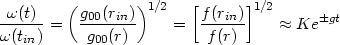(188)

where K is an unimportant constant. It is obvious that the dominant behaviour of (t) will be exponential for any null geodesic starting near the horizon and proceeding away since all the transverse factors will be sub-dominant to the diverging logarithmic singularity arising from the integral of (1/f (r)) near the horizon. Since (t) exp[ ± gt] and the phase (t) of the wave will be vary with time as (t) = <(t) dt exp[ ± gt], the time dependence of the wave at late times will be

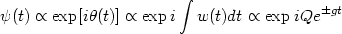(189)

where Q is some constant. An observer at a fixed r will see the wave to have the time dependence exp[i(t)] which, of course, is not monochromatic. If this wave is decomposed into different Fourier components with respect to t, then the amplitude at frequency is given by the Fourier transform

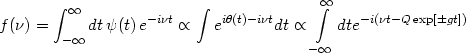(190)

Changing the variables from t to by Qe ^{± gt} = , evaluating the integral by analytic continuation to Im and taking the modulus one finds that the result is a thermal spectrum:

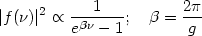(191)

The standard expressions for the temperature are reproduced for Schwarzschild (g = (4M)^-1), de Sitter (g = H) and Rindler spacetimes. This analysis stresses the fact that the origin of thermal spectrum lies in the Fourier transforming of an exponentially red-shifted spectrum.

But in de Sitter or Rindler spacetimes there is no natural notion of "energy source" analogous to the mass of the black-hole. The conventional view is to assume that: (1) In the case of black-holes, one considers the collapse scenario as "physical" and the natural quantum state is the Unruh vacuum. The notions of evaporation, entropy etc. then follow in a concrete manner. The eternal black-hole (and the Hartle-Hawking vacuum state) is taken to be just a mathematical construct not realized in nature. (2) In the case of Rindler, one may like to think of a time-symmetric vacuum state as natural and treat the situation as one of thermal equilibrium. This forbids using quantum states with outgoing radiation which could make the Minkowski spacetime radiate energy - which seems unlikely.

The real trouble arises for spacetimes which are asymptotically de Sitter. Does such a spacetime have temperature and entropy like a collapsing black-hole? Does it "evaporate" ? Everyone is comfortable with the idea of associating temperature with the de Sitter spacetime and most people seem to be willing to associate even an entropy. However, the idea of the cosmological constant changing due to evaporation of the de Sitter spacetime seems too radical. Unfortunately, there is no clear mathematical reason for a dichotomous approach as regards a collapsing black-hole and an asymptotically de Sitter spacetime, since: (i) The temperature and entropy for these spacetimes arise in identical manner due to identical mathematical formalism. It will be surprising if one has entropy while the other does not. (ii) Just as collapsing black hole leads to an asymptotic event horizon, a universe which is dominated by cosmological constant at late times will also lead to a horizon. Just as we can mimic the time dependent effects in a collapsing black hole by a time asymmetric quantum state (say, Unruh vacuum), we can mimic the late time behaviour of an asymptotically de Sitter universe by a corresponding time asymmetric quantum state. Both these states will lead to stress tensor expectation values in which there will be a flux of radiation. (iii) The energy source for expansion at early times (say, matter or radiation) is irrelevant just as the collapse details are irrelevant in the case of a black-hole.

If one treats the de Sitter horizon as a `photosphere' with temperature T = (H / 2) and area A_H = 4 H^-2, then the radiative luminosity will be (dE/dt) T⁴ A_H H². If we take E = (1/2)H^-1, this will lead to a decay law [319] for the cosmological constant of the form:

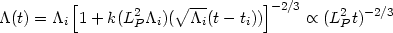(192)

where k is a numerical constant and the second proportionality is for t . It is interesting that this naive model leads to a late time cosmological constant which is independent of the initial value (_i). Unfortunately, its value is still far too large. These issues are not analyzed in adequate detail in the literature and might have important implications for the cosmological constant problem.

---

² This integration can determine the entropy only up to an additive constant. To fix this constant, one can make the additional assumption that S should vanish when M = 0. One may think that this assumption is eminently reasonable since the Schwarzschild metric reduces to the Lorentzian metric when M 0. But note that in the same limit of M 0, the temperature of the black-hole diverges !. Treated as a limit of Schwarzschild spacetime, normal flat spacetime has infinite - rather than zero - temperature. Back.