2.3. Composition of the universe

It is important to stress that absolutely no progress in cosmology can be made until a relationship between and P is provided, say, in the form of the functions w_i(a)s. This fact, in turn, brings to focus two issues which are not often adequately emphasized:

(i) If we assume that the source is made of normal laboratory matter, then the relationship between and P depends on our knowledge of how the equation of state for matter behaves at different energy scales. This information needs to be provided by atomic physics, nuclear physics and particle physics. Cosmological models can at best be only as accurate as the input physics about Tⁱ_k is; any definitive assertion about the state of the universe is misplaced, if the knowledge about Tⁱ_k which it is based on is itself speculative or non existent at the relevant energy scales. At present we have laboratory results testing the behaviour of matter up to about 100 GeV and hence we can, in principle, determine the equation of state for matter up to 100 GeV. By and large, the equation of state for normal matter in this domain can be taken to be that of an ideal fluid with giving the energy density and P giving the pressure; the relation between the two is of the form P = w with w = 0 for non relativistic matter and w = (1/3) for relativistic matter and radiation.

(ii) The situation becomes more complicated when we realize that it is entirely possible for the large scale universe to be dominated by matter whose presence is undetectable at laboratory scales. For example, large scale scalar fields dominated either by kinetic energy or nearly constant potential energy could exist in the universe and will not be easily detectable at laboratory scales. We see from (6) that such systems can have an equation of state of the form P = w with w = 1 (for kinetic energy dominated scalar field) or w = - 1 (for potential energy dominated scalar field). While the conservative procedure for doing cosmology would be to use only known forms of Tⁱ_k on the right hand side of Einstein's equations, this has the drawback of preventing progress in our understanding of nature, since cosmology could possibly be the only testing ground for the existence of forms of Tⁱ_k which are difficult to detect at laboratory scales.

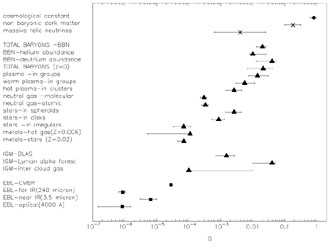Figure 1. Cosmic inventory of energy densities. See text for description. (Figure adapted from [46].)

Figure 1 provides an inventory of the density contributed by different forms of matter in the universe. The x-axis is actually a combination hⁿ of and the Hubble parameter h since different components are measured by different techniques. (Usually n = 1 or 2; numerical values are for h = 0.7.) The density parameter contributed today by visible, non relativistic, baryonic matter in the universe is about _B (0.01 - 0.2) (marked by triangles in the figure; different estimates are from different sources; see for a sample of references [51, 52, 53, 54, 55, 56, 57, 58, 59, 60]). The density parameter due to radiation is about _R 2 × 10^-5 (marked by squares in the figure). Unfortunately, models for the universe with just these two constituents for the energy density are in violent disagreement with observations. It appears to be necessary to postulate the existence of:

• Pressure-less (w = 0) non baryonic dark matter which does not couple with radiation and having a density of about _DM 0.3. Since it does not emit light, it is called dark matter (and marked by a cross in the figure). Several independent techniques like cluster mass-to-light ratios [61] baryon densities in clusters [62, 63] weak lensing of clusters [64, 65] and the existence of massive clusters at high redshift [66] have been used to obtain a handle on _DM. These observations are all consistent with _NR = (_DM + _B) _DM (0.2 - 0.4).
• An exotic form of matter (cosmological constant or something similar) with an equation of state p - (that is, w - 1) having a density parameter of about 0.7 (marked by a filled circle in the figure). The evidence for will be discussed in section 3.

So in addition to H₀, at least four more free parameters are required to describe the background universe at low energies (say, below 50 GeV). These are _B, _R, _DM and describing the fraction of the critical density contributed by baryonic matter, radiation (including relativistic particles like e.g, massive neutrinos; marked by a cross in the figure), dark matter and cosmological constant respectively. The first two certainly exist; the existence of last two is probably suggested by observations and is definitely not contradicted by any observations. Of these, only _R is well constrained and other quantities are plagued by both statistical and systematic errors in their measurements. The top two positions in the contribution to are from cosmological constant and non baryonic dark matter. It is unfortunate that we do not have laboratory evidence for the existence of the first two dominant contributions to the energy density in the universe. (This feature alone could make most of the cosmological paradigm described in this review irrelevant at a future date!)

The simplest model for the universe is based on the assumption that each of the sources which populate the universe has a constant w_i; then equation (20) becomes

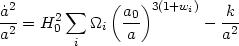(22)

where each of these species is identified by density parameter _i and the equation of state characterized by w_i. The most familiar form of energy densities are those due to pressure-less matter with w_i = 0 (that is, non relativistic matter with rest mass energy density c² dominating over the kinetic energy density, v²/2) and radiation with w_i = (1/3). Whenever any one component of energy density dominates over others, P w and it follows from the equation (22) (taking k = 0, for simplicity) that

(23)

For example, a^-4, a t^1/2 if the source is relativistic and a^-3, a t^2/3 if the source is non-relativistic.

This result shows that the past evolution of the universe is characterized by two important epochs (see eg. [43, 44]): (i) The first is the radiation dominated epoch which occurs at redshifts greater than z_eq (_DM / _R) 10⁴. For z z_eq the energy density is dominated by hot relativistic matter and the universe is very well approximated as a k = 0 model with a(t) t^1/2. (ii) The second phase occurs for z << z_eq in which the universe is dominated by non relativistic matter and - in some cases - the cosmological constant. The form of a(t) in this phase depends on the relative values of _DM and . In the simplest case, with _DM 1, = 0, _B << _DM the expansion is a power law with a(t) t^2/3. (When cosmological constant dominates over matter, a(t) grows exponentially.)

During all the epochs, the temperature of the radiation varies as T a^-1. When the temperature falls below T 10³ K, neutral atomic systems form in the universe and photons decouple from matter. In this scenario, a relic background of such photons with Planckian spectrum at some non-zero temperature will exist in the present day universe. The present theory is, however, unable to predict the value of T at t = t₀; it is therefore a free parameter related _R T⁴₀.