9. GEOMETRICAL STRUCTURE OF THE DE SITTER SPACETIME

The most symmetric vacuum solution to Einstein's equation, of course, is the flat spacetime. If we now add the cosmological constant as the only source of curvature in Einstein's equation, the resulting spacetime is also highly symmetric and has an interesting geometrical structure. In the case of a positive cosmological constant, this is the de Sitter manifold and in the case of negative cosmological constant, it is known as anti-de Sitter manifold. We shall now discuss some features of the former, corresponding to the positive cosmological constant.

To understand the geometrical structure of the de Sitter spacetime, let us begin by noting that a spacetime with the source T_b^a = ^a_b must have 3-dimensional section which are homogeneous and isotropic. This will lead us to the Einstein's equations for a FRW universe with cosmological constant as source

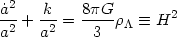(130)

This equation can be solved with any of the following three forms of (k, a(t)) pair. The first pair is the spatially flat universe with (k = 0, a = e^{H t}). The second corresponds to spatially open universe with (k = - 1, a = H^-1sinh H t) and the third will be (k = + 1, a = H^-1cosh H t). Of these, the last pair gives a coordinate system which covers the full de Sitter manifold. In fact, this is the metric on a 4-dimensional hyperboloid, embedded in a 5 dimensional Minkowski space with the metric

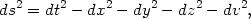(131)

The equation of the hyperboloid in 5-D space is

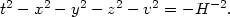(132)

We can introduce a parametric representation of the hyperbola with the four variables (, , , ) where

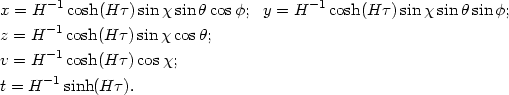(133)

This set, of course, satisfies (132). Using (131), we can compute the metric induced on the hyperboloid which - when expressed in terms of the four coordinates (, , , ) - is given by

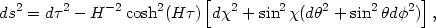(134)

This is precisely the de Sitter manifold with closed spatial sections.

All the three forms of FRW universes with k = 0, ± 1 arise by taking different cuts in this 4-dimensional hyperboloid embedded in the 5-dimensional spacetime. Since two of these dimensions (corresponding to the polar angles and ) merely go for a ride, it is more convenient (for visualization) to work with a 3-dimensional spacetime having the metric

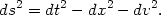(135)

instead of the 5-dimensional metric (131). Every point in this 3-dimensional space corresponds to a 2-sphere whose coordinates and are suppressed for simplicity. The (1 + 1) de Sitter spacetime is the 2-dimensional hyperboloid [instead of the four dimensional hyperboloid of (132)] with the equation

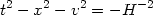(136)

embedded in the 3-dimensional space with metric (135). The three different coordinate systems which are natural on this hyperboloid are the following:

• Closed Spatial Sections: This is obtained by introducing the coordinates t = H^-1sinh(H ); x = H^-1cosh(H ) sin; v = H^-1cosh(H ) cos on the hyperboloid, in terms of which the induced metric on the hyperboloid has the form

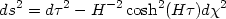  (137)

  This is the two dimensional de Sitter space which is analogous to the 4-dimensional case described by (134).

• Open Spatial Sections: These are obtained by using the coordinates t = H^-1 sinh(H ) cosh; x = H^-1sinh(H ) sinh; v = H^-1cosh(H ) on the hyperboloid in terms of which the induced metric on the hyperboloid has the form

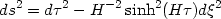  (138)

• Flat Spatial Sections: This corresponds to the choice t = H^-1 sinh(H ) + (H^-1/2) ² exp(H); x = H^-1 cosh(H ) - (H^-1/2) ² exp(H ); v = exp(H ) leading to the metric

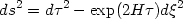  (139)

  This covers one half of the de Sitter hyperboloid bounded by the null rays t + x = 0.

All these metrics have an apparent time dependence. But, in the absence of any source other than cosmological constant, there is no preferred notion of time and the spacetime manifold cannot have any intrinsic time dependence. This is indeed true, in spite of the expansion factor a(t) ostensibly depending on time. The translation along the time direction merely slides the point on the surface of the hyperboloid. [This is obvious in the coordinates (k = 0, a e^{H t}) in which the time translation t t + merely rescales the coordinates by (exp H ).]

The time independence of the metric can be made explicit in another set of coordinates called `static coordinates'. To motivate these coordinates, let us note that a spacetime with only cosmological constant as the source is certainly static and possesses spherical symmetry. Hence we can also express the metric in the form

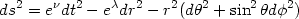(140)

where and are functions of r. The Einstein's equations for this metric has the solution e = e^- = (1 - H² r²) leading to

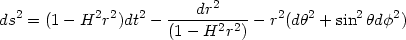(141)

This form of the metric makes the static nature apparent. This metric also describes a hyperboloid embedded in a higher dimensional flat space. For example, in the (1 + 1) case (with , suppressed) this metric can be obtained by the following parameterization of the hyperboloid in equation (136):

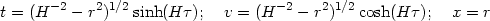(142)

The key feature of the manifold, revealed by equation (141) is the existence of a horizon at r = H^-1. It also shows that t is a time-like coordinate only in the region r < H^-1.

The structure of the metric is very similar to the Schwarzschild metric:

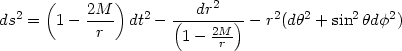(143)

Both the metrics (143) and (141) are spherically symmetric with g₀₀ = - (1/g₁₁). Just as the Schwarzschild metric has a horizon at r = 2M (indicated by g₀₀ 0, g₁₁ ), the de Sitter metric also has a horizon at r = H^-1. From the slope of the light cones (dt / dr) = ± (1 - H² r²)^-1 [corresponding to ds = 0 = d = d in (142)] it is clear that signals sent from the region r < H^-1 cannot go beyond the surface r = H^-1.

This feature, of course, is independent of the coordinate system used. To see how the horizon in de Sitter universe arises in the FRW coordinates, let us recall the equation governing the propagation of light signals between the events (t₁, r₁) and (t, r):

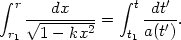(144)

Consider a photon emitted by an observer at the origin at the present epoch (r₁ = 0, t₁ = t₀). The maximum coordinate distance x_H reached by this photon as t is determined by the equation

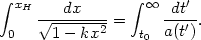(145)

If the integral on the right hand side diverges as t , then, in the same limit, x_H and an observer can send signals to any event provided (s)he waits for a sufficiently long time. But if the integral on the right hand side converges to a finite value as t , then there is a finite horizon radius beyond which the observer's signals will not reach even if (s)he waits for infinite time. In the de Sitter universe with k = 0 and a(t) = e^{H t}, x_H = H^-1 e^{-H t₀}; the corresponding maximum proper distance up to which the signals can reach is r_H = a(t₀) x_H = H^-1. Thus we get the same result in any other coordinate system.

Since the result depends essentially on the behaviour of a(t) as t , it will persist even in the case of a universe containing both non relativistic matter and cosmological constant. For example, in our universe, we can ask what is the highest redshift source from which we can ever receive a light signal, if the signal was sent today. To compute this explicitly, consider a model with _NR + = 1. Let us assume that light from an event at (r_H, z_H) reaches r = 0 at z = 0 giving

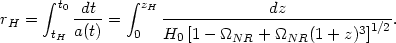(146)

If we take r_H to be the size of the horizon, then it also follows that the light emitted today from this event will just reach us at t = . This gives

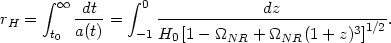(147)

Equating the two expressions, we get an implicit expression for z_H. If _NR = 0.3, the limiting redshift is quite small: z_H 1.8. This implies that sources with z > z_H can never be influenced by light signals from us in a model with cosmological constant [286, 287].