


The basic tenet that governs cosmology is known as the cosmological principle. This principle states that, on large scales, the present universe is homogeneous and isotropic. Homogeneity means that the properties of the universe are the same everywhere in the universe; and isotropy means that from every point, the properties of the universe are the same in every direction. It can be shown that the cosmological principle alone requires that the metric tensor of the universe must take the form of the Robertson-Walker metric. [1] In co-moving, spherical coordinates, this metric tensor leads to the well known line element
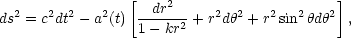 |
(1) |
where the dimensionless function a(t) is called the cosmic scale factor. This line element describes an expanding (or contracting) universe that, at the present (or any) instant in time t0, is a three-dimensional hypersphere of constant scalar curvature K(t0) = k / a2(t0). The parameter k represents the sign of this constant which can either be positive (k = + 1 m-2), negative (k = - 1 m-2), or zero (k = 0).
The dynamics of the universe is governed by the Einstein field equations
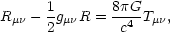 |
(2) |
where
Rµ is
the Ricci tensor, R is the scalar curvature, and
Tµ
is
the Ricci tensor, R is the scalar curvature, and
Tµ is
the stress-energy tensor. On large scales, the stress-energy
tensor of the universe is taken to be that of a perfect fluid (since
homogeneity and isotropy imply that there is no bulk energy transport)
is
the stress-energy tensor. On large scales, the stress-energy
tensor of the universe is taken to be that of a perfect fluid (since
homogeneity and isotropy imply that there is no bulk energy transport)
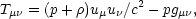 |
(3) |
where uµis the four-velocity of the fluid,
 is its energy
density, and p is the fluid pressure. In Eqs. (2) and (3),
gµ
is its energy
density, and p is the fluid pressure. In Eqs. (2) and (3),
gµ is
relative to the Cartesian coordinates (x0 = ct,
x1 = x,
x2 = y, x3 = z).
Under the restrictions imposed by the cosmological principle, the field
equations (2) reduce to the Friedmann equations for the cosmic scale
factor
is
relative to the Cartesian coordinates (x0 = ct,
x1 = x,
x2 = y, x3 = z).
Under the restrictions imposed by the cosmological principle, the field
equations (2) reduce to the Friedmann equations for the cosmic scale
factor
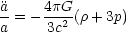 |
(4) |
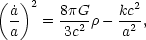 |
(5) |
where the dot notation represents a derivative with respect to time, as is customary. Observationally, it is known that the universe is expanding. The expansion of the universe follows the Hubble law
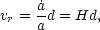 |
(6) |
where vr is the speed of recession between two points,
d is the proper distance between these points, and
H( 
 /a) is
called the Hubble parameter. One of the key features of the Hubble
law is that, at any given instant, the speed of recession is directly
proportional to the distance. Therefore, by analyzing the Doppler shift
in the light from a distant source we can infer its distance provided
that we know the present value of the Hubble parameter
H0, called the Hubble constant.
[2]
/a) is
called the Hubble parameter. One of the key features of the Hubble
law is that, at any given instant, the speed of recession is directly
proportional to the distance. Therefore, by analyzing the Doppler shift
in the light from a distant source we can infer its distance provided
that we know the present value of the Hubble parameter
H0, called the Hubble constant.
[2]
One of the principal questions that the field of cosmology hopes to answer concerns the ultimate fate of the universe. Will the universe expand forever, or will the expansion halt and be followed by a contraction? This question of the long-term fate of the expansion is closely connected to the sign of k in the Friedmann equation (5). General relativity teaches us that the curvature of spacetime is determined by the density of matter and energy. Therefore, the two terms on the right-hand-side of Eq. (5) are not independent. The value of the energy density will determine the curvature of spacetime and, consequently, the ultimate fate of the expansion. Recognizing that the left-hand-side of Eq. (5) is H2, we can rewrite this expression as
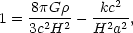 |
(7) |
and make the following definition:
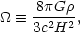 |
(8) |
called the density parameter.
Since the sum of the density and curvature terms in Eq. (7) equals
unity, the case for which
 < 1 corresponds
to a negative curvature term requiring k = - 1
m-2. The solution for negative
curvature is such that the universe expands forever with excess velocity
< 1 corresponds
to a negative curvature term requiring k = - 1
m-2. The solution for negative
curvature is such that the universe expands forever with excess velocity
 t=
t= > 0. This latter
case is referred to as an open
universe. The case for which corresponds to a positive curvature term
requiring k = + 1 m-2. The solution for positive
curvature (a closed universe) is such that the expansion
eventually halts and becomes a universal contraction leading to what is
known as the big crunch. Finally, the case for which
> 0. This latter
case is referred to as an open
universe. The case for which corresponds to a positive curvature term
requiring k = + 1 m-2. The solution for positive
curvature (a closed universe) is such that the expansion
eventually halts and becomes a universal contraction leading to what is
known as the big crunch. Finally, the case for which
 = 1 corresponds to zero
curvature (a flat universe) requiring k = 0. The solution
for a flat universe is the critical case that lies on the boundary
between an
open and closed universe. In this case, the universe expands forever,
but the rate of expansion approaches zero asymptotically,
= 1 corresponds to zero
curvature (a flat universe) requiring k = 0. The solution
for a flat universe is the critical case that lies on the boundary
between an
open and closed universe. In this case, the universe expands forever,
but the rate of expansion approaches zero asymptotically,
 t=
t= = 0. The value of the
energy density for which
= 0. The value of the
energy density for which
 = 1 is called the
critical density
= 1 is called the
critical density  c , given by
c , given by
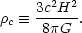 |
(9) |
The density parameter, then, is the ratio of the energy density of the
universe to the critical density
 =
=
 /
/
 c.
c.
There is one final parameter that is used to characterize the universal
expansion. Notice that Eq. (4) expresses the basic result that in a
matter-dominated universe (in which
 + 3p
> 0) the expansion should be decelerating,
+ 3p
> 0) the expansion should be decelerating,
 < 0, as a result of
the collective
gravitational attraction of the matter and energy in the universe. This
behavior is characterized by the deceleration parameter
< 0, as a result of
the collective
gravitational attraction of the matter and energy in the universe. This
behavior is characterized by the deceleration parameter
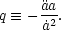 |
(10) |
The matter in the present universe is very sparse, so that it is effectively noninteracting (i.e., dust). Therefore, it is generally assumed that the fluid pressure, p, is negligible compared to the energy density. Under these conditions, Eq. (4) shows that the deceleration parameter has a straightforward relationship to the density parameter
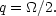 |
(11) |
Collectively, the Hubble constant H0 and the present
values of the density parameter
 0 and the
deceleration parameter q0 are
known as the cosmological parameters. These parameters are chosen,
in part, because they are potentially measurable. The range of values
that correspond to the different fates of the universe, within this
traditional framework, are summarized in Table 1.
0 and the
deceleration parameter q0 are
known as the cosmological parameters. These parameters are chosen,
in part, because they are potentially measurable. The range of values
that correspond to the different fates of the universe, within this
traditional framework, are summarized in Table 1.
| Model | Parameters | ||
| 50 < H0 < 100 km . s-1 . Mpc-1 | |||
| Open |  < 1
< 1 |
 m < m <
 c c |
q0 < 1/2 |
| Closed |  > 1
> 1 |
 m > m >
 c c |
q0 > 1/2 |
| Flat |  = 1
= 1 |
 m = m =
 c c |
q0 = 1/2 |
The understanding of cosmology, as outlined above, left several questions unanswered, including the fate of the universal expansion. It was entirely possible to formulate reasonable arguments for whether or not the universe is open, closed, or flat that covered all three possibilities. The observational data has always suggested that the density of visible matter is insufficient to close the universe and researchers choosing to side with the data could easily take the position that the universe is open. However, it has been known for several decades that a substantial amount of the matter in the universe, perhaps even most of it, is not visible. The existence of large amounts of dark matter can be inferred from its gravitational effects both on and within galaxies. [3] Therefore, the prospects of dark matter (and neutrino mass) rendered any conclusion based solely on the amount of visible matter premature. Einstein's view was that the universe is closed, apparently for reasons having to do with Mach's principle [4], and many researchers preferred this view as well for reasons that were sometimes more philosophical than scientific. Then, there were also hints that the universe may be flat; consequentially, many researchers believed that this was most likely true.
Belief that the universe is flat was partly justified by what is known
in cosmology as the flatness problem having to do with the
apparent need of the universe to have been exceedingly close to the
critical density shortly after the big bang. The fate of the universe
and the flatness problem are just two of several puzzles that emerge
from this standard model of the universe. Another important puzzle has
to do with the existence, or nonexistence, of the cosmological
constant,  . It turns out that
. It turns out that
 plays a very
important role in our story, and its story must be told before we can
explain how cosmologists have pinned down some of the basic properties
of the universe.
plays a very
important role in our story, and its story must be told before we can
explain how cosmologists have pinned down some of the basic properties
of the universe.