3.3. Faraday Rotation Measurements

To infer the magnitude of the magnetic field strength Faraday effect has been widely used. When a polarized radio wave passes through a region of space of size containing a plasma with a magnetic field the polarization plane of the wave gets rotated by an amount

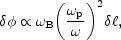(3.7)

which is directly proportional to the square of the plasma frequency ⁽⁸⁾ _p (and hence to the electron density) and to the Larmor frequency _B (and hence to the magnetic field intensity). A linear regression connecting the shift in the polarization plane and the square of the wavelength , can be obtained:

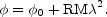(3.8)

By measuring the relation expressed by Eq. (3.8) for two (or more) separate (but close) wavelengths, the angular coefficient of the regression can be obtained and it turns out to be

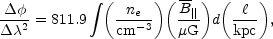(3.9)

in units of rad/m² when all the quantities of the integrand are measured in the above units. The explicit dependence of the red-shift can be also easily included in Eq. (3.9). Notice, in general terms that the RM is an integral over distances. Thus the effect of large distances will reflect in high values of the RM. Furthermore, the Faraday effect occurs typically in the radio (i.e. cm < < m), however, some possible applications of Faraday effect in the microwave can be also expected (see Section 8 of the present review).

The shift in the polarization plane should be determined with an accuracy greater than ~ ± . Otherwise ambiguities may arise in the determination of the angular coefficient appearing in the linear regression of Eq. (3.8).

This aspect is illustrated in Fig. 1 which is rather standard but it is reproduced here in order to stress the possible problems arising in the physical determination of the RM if the determination of the shift in the polarization plane is not accurate.

Figure 1. The possible ambiguities arising in practical determinations of the RM are illustrated. The RM is the angular coefficient of the linear regression expressed by Eq. (3.8). Clearly it is not necessary to know the initial polarization of the source to determine the slope of a straight line in the (, 2) plane, but it is enough to measure at two separate wavelength. However, if the accuracy in the determination of is of the order of the inferred determination of the angular coefficient of the linear regression (3.8) is ambiguous.

The RM defined in Eq. (3.9) not only the magnetic field (which should be observationally estimated), but also the column density of electrons. From the radio-astronomical observations, different techniques can be used in order to determine n_e. One possibility is to notice that in the observed Universe there are pulsars. Pulsars are astrophysical objects emitting regular pulses of electromagnetic radiation with periods ranging from few milliseconds to few seconds. By comparing the arrival times of different radio pulses at different radio wavelengths, it is found that signals are slightly delayed as they pass through the interstellar medium exactly because electromagnetic waves travel faster in the vacuum than in an ionized medium. Hence, from pulsars the column density of electrons can be obtained in the form of the dispersion measure, i.e. DM n_e d. Dividing the RM by DM, an estimate of the magnetic field can be obtained. Due to their abundance, pulsars lead to the best determination of the magnetic field in the galactic disk [30].

In Fig. 2 (adapted from [31]) a map of the antisymmetric RM sky is reported. In the picture the open circles denote negative RM while filled circles denote positive RM. The size of the circle is proportional to the magnitude of the RM. The convention is, in fact, to attribute negative RM to a magnetic field directed away from the observer and positive RM if the magnetic field is directed toward the observer.

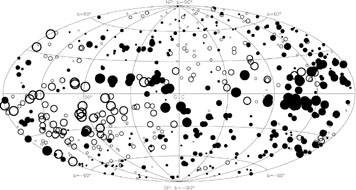Figure 2. The filtered RM distribution of extragalactic radio sources. The antisymmetric distribution is clear especially from the inner galactic quadrant. This picture is adapted from [31].

As in the case of synchrotron emission also Faraday rotation measurements can be used as a diagnostic for foreground contamination. The idea would be, in this context to look for cross-correlations in the Faraday rotation measure of extra-galactic sources and the measured microwave signal at the same angular position. A recent analysis has been recently reported [32].

If magnetic field or the column density change considerably over the integration path of Eq. (3.9) one should probably define and use the two-point function of the RM, i.e.

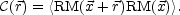(3.10)

The suggestion to study the mean-squared fluctuation of the RM was proposed [33, 34]. More recently, using this statistical approach particularly appropriate in the case of magnetic fields in clusters (where both the magnetic field intensity and the electron density change over the integration path), Newmann, Newmann and Rephaeli [35] quantified the possible (statistical) uncertainty in the determination of cluster magnetic fields (this point will also be discussed later). The rather ambitious program of measuring the RM power spectrum is also pursued [36, 37]. In [38] the analysis of correlations in the RM has been discussed.

⁸ See Eq. (4.5) in the following Section. Back.