


4.5. Magnetic diffusivity equation
From Eqs. (4.22) and (4.23) the Ohmic electric field can be expressed as
 |
(4.28) |
which inserted into Eq. (4.19) leads to the magnetic diffusivity equation
 |
(4.29) |
The first term of Eq. (4.29) is the dynamo term. The second term of Eq. (4.29) is the magnetic diffusivity term whose effect is to dissipate the magnetic field. By comparing the left and the right hand side of Eq. (4.29), the typical time scale of resistive phenomena is
 |
(4.30) |
where L is the typical length scale of the magnetic field. In a
non-relativistic plasma
the conductivity  goes
typically as T3/2
[85].
In the case of planets, like the earth, one can wonder why a sizable
magnetic field can still be present. One of
the theories is that the dynamo term regenerates continuously
the magnetic field which is dissipated by the diffusivity term
[20].
In the case of the galactic disk the value of the conductivity
(13) is given by
goes
typically as T3/2
[85].
In the case of planets, like the earth, one can wonder why a sizable
magnetic field can still be present. One of
the theories is that the dynamo term regenerates continuously
the magnetic field which is dissipated by the diffusivity term
[20].
In the case of the galactic disk the value of the conductivity
(13) is given by

 7 ×
10-7 Hz. Thus, for
L
7 ×
10-7 Hz. Thus, for
L  kpc
t
kpc
t
 109(L
/ kpc)2 sec.
109(L
/ kpc)2 sec.
In Eq. (4.30) the typical time of resistive phenomena has been introduced. Eq. (4.30) can also give the typical resistive length scale once the time-scale of the system is specified. Suppose that the time-scale of the system is given by tU ~ H0-1 ~ 1018 sec where H0 is the present value off the Hubble parameter. Then
 |
(4.31) |
leading to
L ~
AU. The scale (4.31) gives then the
upper limit on the diffusion scale for a magnetic field whose lifetime is
comparable with the age of the Universe at the present epoch. Magnetic
fields with typical correlation scale larger than
L
~
AU. The scale (4.31) gives then the
upper limit on the diffusion scale for a magnetic field whose lifetime is
comparable with the age of the Universe at the present epoch. Magnetic
fields with typical correlation scale larger than
L are
not affected by resistivity. On the other
hand, magnetic fields with typical correlation scale L <
L
are
not affected by resistivity. On the other
hand, magnetic fields with typical correlation scale L <
L are
diffused. The value
L
are
diffused. The value
L ~ AU
is consistent with the phenomenological
evidence that there are no magnetic fields coherent over scales smaller
than 10-5 pc.
~ AU
is consistent with the phenomenological
evidence that there are no magnetic fields coherent over scales smaller
than 10-5 pc.
The dynamo term may be responsible for the origin of the magnetic field
of the galaxy. The galaxy has a typical rotation period of
3 × 108 yrs and comparing this number with the typical
age of the galaxy,
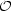 (1010 yrs),
it can be appreciated that the galaxy performed about 30 rotations since
the time of the protogalactic collapse.
(1010 yrs),
it can be appreciated that the galaxy performed about 30 rotations since
the time of the protogalactic collapse.
From Eq. (4.29) the usual structure of the dynamo term may be derived
by carefully averaging
over the velocity filed according to the procedure of
[89,
90].
By assuming that the motion of the fluid is random and with zero mean
velocity the average is taken over the ensemble of the possible
velocity fields.
In more physical terms this averaging procedure of Eq. (4.29) is
equivalent to average over scales and times exceeding the
characteristic correlation scale and time
 0 of the velocity
field. This procedure assumes that the correlation scale of the
magnetic field is much bigger than the correlation scale of the
velocity field which is required to be divergence-less
(
0 of the velocity
field. This procedure assumes that the correlation scale of the
magnetic field is much bigger than the correlation scale of the
velocity field which is required to be divergence-less
(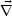 .
.
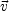 = 0).
In this approximation the magnetic diffusivity equation can be written
as:
= 0).
In this approximation the magnetic diffusivity equation can be written
as:
 |
(4.32) |
where
 |
(4.33) |
is the so-called dynamo term which vanishes
in the absence of vorticity. In Eqs. (4.32)-(4.33)
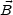 is
the magnetic field averaged over times longer that
is
the magnetic field averaged over times longer that
 0 which is the
typical correlation time of the velocity field.
0 which is the
typical correlation time of the velocity field.
It can be argued that the essential
requirement for the consistence of the mentioned averaging procedure is
that the turbulent velocity field has to be "globally" non-mirror
symmetric
[19].
If the system would
be, globally, invariant under parity transformations, then, the
 term would
simply vanish. This observation is related to the turbulent features
of cosmic systems. In cosmic turbulence the systems are
usually rotating and, moreover, they possess a gradient in the
matter density (think, for instance, to the case of the galaxy). It is then
plausible that parity is broken at the level of the galaxy since terms
like
term would
simply vanish. This observation is related to the turbulent features
of cosmic systems. In cosmic turbulence the systems are
usually rotating and, moreover, they possess a gradient in the
matter density (think, for instance, to the case of the galaxy). It is then
plausible that parity is broken at the level of the galaxy since terms
like 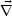
 m
.
m
.
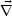 ×
×
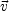 are not vanishing
[19].
are not vanishing
[19].
The dynamo term, as it appears in Eq. (4.32), has a simple electrodynamical meaning, namely, it can be interpreted as a mean ohmic current directed along the magnetic field :
 |
(4.34) |
This equation tells us that an ensemble of screw-like vortices with zero mean helicity is able to generate loops in the magnetic flux tubes in a plane orthogonal to the one of the original field. Consider, as a simple application of Eq. (4.32), the case where the magnetic field profile is given by
 |
(4.35) |
For this profile the magnetic gyrotropy is non-vanishing, i.e.
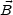 .
.
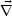 ×
×
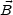 = k
f2(t). From Eq. (4.32), using Eq. (4.35)
f (t) obeys the following equation
= k
f2(t). From Eq. (4.32), using Eq. (4.35)
f (t) obeys the following equation
 |
(4.36) |
admits exponentially growing solutions for sufficiently large scales, i.e.
k < 4 |
| |
|
 .
Notice that in this naive example the
.
Notice that in this naive example the
 term is assumed to be
constant. However, as the amplification proceeds,
term is assumed to be
constant. However, as the amplification proceeds,
 may develop a
dependence upon
|
may develop a
dependence upon
|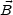 |2,
i.e.
|2,
i.e. 

 0(1 -
0(1 -
 |
|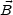 |2)
|2)
 0[1 -
0[1 -
 f2(t)]. In the case
of Eq. (4.36) this modification will introduce non-linear terms whose
effect will be to stop the growth of the magnetic field.
This regime is often called saturation of the dynamo and the non-linear
equations appearing in this context are sometimes called Landau equations
[19]
in analogy with the Landau equations appearing in hydrodynamical turbulence.
f2(t)]. In the case
of Eq. (4.36) this modification will introduce non-linear terms whose
effect will be to stop the growth of the magnetic field.
This regime is often called saturation of the dynamo and the non-linear
equations appearing in this context are sometimes called Landau equations
[19]
in analogy with the Landau equations appearing in hydrodynamical turbulence.
In spite of the fact that in the previous example the velocity field has been averaged, its evolution obeys the Navier-Stokes equation
 |
(4.37) |
where  is the thermal
viscosity coefficient. Since in MHD the matter current is solenoidal
(i.e.
is the thermal
viscosity coefficient. Since in MHD the matter current is solenoidal
(i.e. 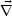 .(
.(
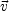 ) = 0) the
incompressible closure
) = 0) the
incompressible closure
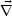
 = 0, corresponds
to a solenoidal velocity field
= 0, corresponds
to a solenoidal velocity field
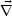 .
. 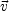 = 0.
Recalling Eq. (4.22), the Lorentz force term can be re-expressed through
vector identities and Eq. (4.37) becomes
= 0.
Recalling Eq. (4.22), the Lorentz force term can be re-expressed through
vector identities and Eq. (4.37) becomes
 |
(4.38) |
In typical applications to the evolution of magnetic fields prior to
recombination the magnetic pressure term is always smaller than the
fluid pressure (14), i.e.
p >>
|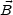 |2.
Furthermore, there are cases where the Lorentz force term can be
ignored. This is the so-called force free approximation. Defining the
kinetic helicity as
|2.
Furthermore, there are cases where the Lorentz force term can be
ignored. This is the so-called force free approximation. Defining the
kinetic helicity as
 =
=
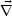 ×
×
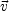 ,
the magnetic diffusivity and Navier-Stokes equations can be written in a
rather simple and symmetric form
,
the magnetic diffusivity and Navier-Stokes equations can be written in a
rather simple and symmetric form
 |
(4.39) |
In MHD various dimensionless ratios can be defined. The most frequently used are the magnetic Reynolds number, the kinetic Reynolds number and the Prandtl number:
 |
(4.40) (4.41) (4.42) |
where LB and Lv are the typical
scales of variation of the magnetic and velocity fields.
In the absence of pressure and density perturbations
the combined system of Eqs. (4.22) and (4.38) can be linearized easily.
Using then the incompressible closure the propagating modes are the
Alfvén waves whose typical dispersion relation is
 2 =
ca2 k2 where
ca =
|
2 =
ca2 k2 where
ca =
|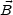 | /
(4
| /
(4
 )1/2.
Often the Lundqvist number is called, in plasma literature
[85,
87]
magnetic Reynolds number. This confusion arises from the
fact that the Lunqvist number, i.e. ca L
)1/2.
Often the Lundqvist number is called, in plasma literature
[85,
87]
magnetic Reynolds number. This confusion arises from the
fact that the Lunqvist number, i.e. ca L
 , is the magnetic
Reynolds number when v coincides with the Alfvén
velocity. To have a very large Lundqvist number implies that the the
conductivity is very large. In this sense the Lunqvist number
characterizes, in fusion theory, the rate of growth of resistive
instabilities and it is not necessarily related to the possible
occurrence of turbulent dynamics.
On the contrary, as large Reynolds numbers are related to the occurrence of
hydrodynamical turbulence, large magnetic Reynolds numbers are
related to the occurence of MHD turbulence
[87].
, is the magnetic
Reynolds number when v coincides with the Alfvén
velocity. To have a very large Lundqvist number implies that the the
conductivity is very large. In this sense the Lunqvist number
characterizes, in fusion theory, the rate of growth of resistive
instabilities and it is not necessarily related to the possible
occurrence of turbulent dynamics.
On the contrary, as large Reynolds numbers are related to the occurrence of
hydrodynamical turbulence, large magnetic Reynolds numbers are
related to the occurence of MHD turbulence
[87].
13 It is common use in the astrophysical
applications to work directly with
 =
(4
=
(4
 )-1. In the
case of the galactic disks
)-1. In the
case of the galactic disks
 =
1026 cm2 Hz. The variable
=
1026 cm2 Hz. The variable
 denotes, in the
present review, the conformal time coordinate.
Back.
denotes, in the
present review, the conformal time coordinate.
Back.
14 Recall that in fusion studies the
quantity  =
8
=
8 |
|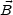 |2 /
p is usually defined. If the plasma is confined, then
|2 /
p is usually defined. If the plasma is confined, then
 is of order
1. On the contrary, if
is of order
1. On the contrary, if
 >> 1,
as implied by the critical density bound in the early Universe, then the
plasma may be compressed at higher temperatures and densities.
Back.
>> 1,
as implied by the critical density bound in the early Universe, then the
plasma may be compressed at higher temperatures and densities.
Back.