5. ORBITAL DECAY AND "CANNIBALISM"

Given that the tidal field of a rich cluster is so efficient at limiting the sizes of galactic halos, it makes sense, at least to first order, to ignore encounters between galaxies when considering how clusters might evolve dynamically after their formation. In this simple model, the most important physical process that acts to modify the orbital motion of galaxies is dynamical friction (Chandrasekhar 1943), the force that results from polarization of the dark matter as a galaxy moves through it. Roughly speaking, every galaxy is followed in its orbit by a "wake" of slight overdensity that produces a constant deceleration; as the galaxy loses kinetic energy to the dark matter, its orbit decays. The equation of motion of a galaxy in a spherical cluster that is dominated by smoothly-distributed dark matter is, in Chandrasekhar's (1943) local approximation,

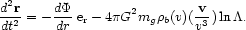(22)

The first term on the right-hand side of equation (22) defines the unperturbed motion of the galaxy in the cluster potential (r). The second term is the drag force: m_g and v are the galaxy mass and velocity; _b(v) is the density of "background" particles with velocities, relative to the cluster center of mass, less than the orbital velocity v; and ln is the "Coulomb logarithm", about equal to 3 in the present context.

Equation (22) (which should be viewed as a rough approximation; see e.g. White 1983) predicts that galaxies which orbit in regions of the highest darkmatter density will undergo the most rapid orbital decay. Consider therefore a galaxy whose orbit is confined to the cluster core. If the dark matter in the core is uniformly distributed with density ₀, then the galaxy sees a potential which is nearly harmonic,

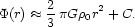(23)

The drag force, assuming a Maxwellian distribution of background particle velocities, is

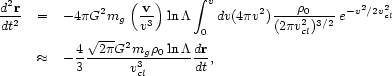(24)

where v_cl is the one-dimensional velocity dispersion of the dark-matter "particles" (probably roughly equal to the velocity dispersion of the bright galaxies). The equation describing the galaxy's orbit is then

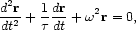(25)

where

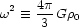(26)

and

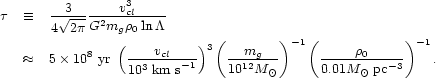(27)

Equation (25), which is the equation of a damped harmonic oscillator, states that the orbits of galaxies in cluster cores will decay with a time constant ~ 2r; furthermore, the orbits retain their shape as they shrink. (The orbits of galaxies that spend most of their time outside of the core tend to circularize as they shrink; however the orbital decay time for these galaxies greatly exceeds a Hubble time.) If we assume that galaxies retain as much matter in their halos as the tidal field permits, then the decay time becomes (equations (14), (27)):

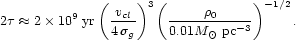(28)

Thus the orbits of bright galaxies in and near the core may have decayed appreciably since the epoch of cluster formation. What are the observable consequences of this decay? Since the decay time is inversely proportional to galaxy mass, we would expect the most massive galaxies to fall to the cluster center most quickly. Insofar as a galaxy's mass is correlated with its luminosity - a big "if", given that most of the matter is dark - the bright galaxies should therefore be more centrally concentrated and have lower orbital velocities than the faint galaxies. This "luminosity segregation" should not be terribly striking, however, because it is a differential effect, and because decay times are likely to be comparable to cluster lifetimes for all but the brightest galaxies. Figure 5 shows the dependence of orbital velocity dispersion on galaxy luminosity for galaxies near the center of the Coma cluster. Also shown are the predicted dependences, at times {0.6, 2, 6, 20} × ^*, for an initially isothermal cluster with a Schechter (1976) luminosity function; here ^* is the decay time of an L^* galaxy. The predicted amount of segregation, even in the extreme models, is small compared with the statistical uncertainties. Other studies (e.g. Rood 1965; White 1977) have similarly concluded that luminosity segregation in the Coma cluster is too small to be detected.

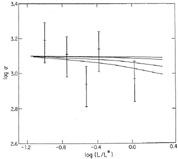Figure 5. Orbital velocity dispersion as a function of luminosity for galaxies within 0.35h-1 Mpc of the center of the Coma cluster. Solid line: predicted dependence, at four times, for an initially isothermal cluster with a Schechter luminosity function. (From Merritt, Ap. J., 276, 26)

A second, potentially observable consequence of orbital decay is that bright galaxies as a group should accumulate at the cluster center. It may be shown (Merritt 1984b) that in an initially isothermal cluster, the central density of a group of galaxies of mass m₁ will increase with time constant

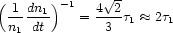(29)

for t ; at later times the accumulation slows. Thus we might expect that the central density of the brighter galaxies will increase by a factor of ~ a few in a Hubble time. Such an enhancement has probably been observed. Beers and Tonry (1986) find that the combined density profile of a set of ~ 35 rich clusters is well described by a power law, r^-2, even at relatively small radii 0.25h^-1 Mpc, as long as the cluster centers are assumed to coincide with either the location of a cD galaxy, or the peak of the X-ray surface brightness. Figure 6 shows the Beers and Tonry (1986) data, as well as the projected number density profiles of three initially isothermal clusters, containing equalmass galaxies, which have been evolved for times {0, 2, 3} × . It is clear that moderate amounts of orbital decay (corresponding to times 2 - 3) are sufficient to "erase" the core and produce a density profile similar to that found by Beers and Tonry.

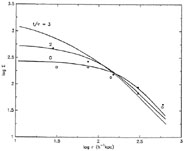Figure 6. Cluster surface density profiles. Squares: Beers and Tonry's (1986) combined profile, computed by superposing 36 clusters centered on the peak of their X-ray surface brightness profiles; circles: density profile of 49 clusters superposed on their median centers. Solid lines: density profiles of an initially isothermal cluster in which the galaxy orbits decay due to dynamical friction.

A third possible consequence of orbital decay, and by far the most interesting, is the formation of a very bright galaxy at the center of a cluster through the repeated accretion of other galaxies which spiral in. This is the so-called "cannibalism" model; its primary motivation is the existence, at the centers of roughly 10% of rich clusters, of very bright (L 5L^*) or "cD" galaxies. In almost every respect, the properties of cD galaxies appear to lie along a smooth continuation of the trends defined by less luminous galaxies (Tonry 1987). However, the fact that they are always located precisely at the centers of clusters, both spatially (Beers and Geller 1983) and kinematically (Quintana and Lawrie 1982), hints at a special formation process. Broadly speaking, theories which attempt to explain the central locations and high luminosities of cD galaxies by invoking mergers in cluster cores can be divided into two groups, which collectively define what might be called the "weak" and "strong" theories of cannibalism. According to the "weak" cannibalism hypothesis (Ostriker and Tremaine 1975), a massive galaxy which happens to lie near the center of a cluster will undergo a significant, although modest, increase in luminosity over a Hubble time as it accretes less massive neighbors and bound satellites. According to the "strong" cannibalism hypothesis (White 1976; Hausman and Ostriker 1978), orbital decay and merger times are sufficiently short that a superluminous galaxy will naturally form at the center of any rich relaxed cluster after about 10¹⁰ years. In its most extreme form (Hausman and Ostriker 1978), the "strong" hypothesis states that the sequence of cluster types, as described by Bautz and Morgan (1970) or Oemler (1974), is one of increasing dynamical evolution, the rate of evolution being fixed by the central orbital decay time.

At present these is no consensus about which (if either) of these hypotheses is correct. Numerous attempts have been made to simulate the evolution of a rich cluster after its formation (e.g. Richstone and Malumuth 1983; Malumuth and Richstone 1984; Merritt 1984a, 1985), but with very different results. The disagreement stems mostly from. the fact that a galaxy cluster is a very inhomogeneous system, containing matter with a wide range of densities; thus a self-consistent approach is essentially impossible with existing computers. Instead, one is forced to represent cluster galaxies by a small set of parameters (e.g. mass, radius, orbital energy and angular momentum), which vary discontinously as a result of interactions with other galaxies and with the dark matter. The cross sections and efficiencies of the various physical processes (e.g. tidal truncation, collisional mass loss, mergers) must be specified at 'the outset as a function of these parameters. It is only relatively recently that accurate cross-sections for these. processes have become available; most published simulations of cluster evolution have been based on extrapolations from a handful of relatively crude N-body simulations.

In the absence of a good theoretical understanding of cluster evolution, it is reasonable to ask what constraints the observations place on the cannibalism hypothesis. By far the strongest evidence for ongoing merging in rich clusters comes from the large numbers of first-ranked galaxies which are observed to contain two or more "nuclei" within a single envelope. The extra "nuclei" have traditionally been interpreted as cluster galaxies that are gravitationally bound to the central giant and in the process of merging with it. Recent studies (Hoessel 1980; Schneider, Gunn and Hoessel 1983) have shown that the probability,of finding a second "nucleus" very near the center of a first-ranked galaxy is two or three times greater than would be expected from random projection against a uniform cluster core. Converting the observed overdensity into a merger rate is difficult, however, without a detailed understanding of the merger process. Figure 7 illustrates the problem with a simple model. That figure shows the evolution, due to orbital decay, of the same initially-isothermal cluster of Figure 6, except that now a central galaxy of mass ~ 1.5 × 10¹² M has been added at the center. At early times, t , the number of galaxies seen close to the cluster center is enhanced, due to the additional frictional force from the central giant. At later times, however, the rate of infall of galaxies from outside the core is nearly matched by the rate at which they are "eaten", with the result that their density near the giant remains nearly constant. Although the "cannibal" continues to grow, this growth is not accompanied by an increase in the density of galaxies near to it. Also, since low-velocity galaxies are quickly accreted, the orbital velocities of the yet-unaccreted galaxies remain high, comparable to that of the other galaxies in the cluster. This simple model is consistent with the multiple-nucleus observations, both in terms of the observed overdensity, and the velocity dispersion of the nuclei (Tonry 1984). However it is clear from Figure 7 that we cannot hope to use statistics of the "nuclei" to derive the current merger rate, since the two are nearly uncoupled once a moderate amount of orbital decay has taken place.

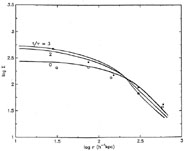Figure 7. Like Fig. 6, except that a 1.5 × 1012 M galaxy has been added to the center of the model cluster.

Recently Lauer (1988) has shown a way around this problem. He observed the morphology of a set of 16 multiple-nucleus galaxies, and attempted to model each one as a superposition of normal "secondaries" seen against the brighter "primary". Roughly half of the systems could be convincingly modelled in this way; the other half showed evidence for distortions that presumably indicate tidal perturbations. Assuming that all of the "nuclei" in the latter group are in the process of being captured by their primaries, and that the typical merger time is ~ 3 × 10⁸ yr, Lauer estimated that the current rate of growth of an average first-ranked cluster galaxy is ~ 2L^* / 5 × 10⁹ yr. This growth rate is insufficient to produce a superluminous (L 10L^*) galaxy in a cluster that did not contain one initially, especially since, in the simple model for orbital decay outlined above, the current infall rate is always larger than the time averaged rate. Taken at face value, therefore, Lauer's result suggests that the "weak" cannibalism hypothesis is more correct, i.e., that cD galaxies grow by only moderate amounts over a cluster lifetime.

It follows that, if mergers were important in the formation of cD galaxiesand this seems a priori very likely, if only because cD's are so large and brightthen these mergers must have taken place at a time when their environments were very different than they are now. In fact it has been shown via Nbody simulations (e.g. Barnes 1985 that galaxies in small dense groups tend to merge very quickly. Since rich clusters probably formed from the amalgamation of smaller groups (e.g. Layzer 1954), it may well be that cD galaxies acquired most of their mass and luminosity during the epoch preceding cluster formation, rather than later.