Annu. Rev. Astron. Astrophys. 2000. 38: 289-335 Copyright © 2000 by Annual Reviews. All rights reserved

4.2. L_X- and L_X-T Relations

Strong correlations are also found between X-ray luminosity and both velocity dispersion and gas temperature in groups. However, there is considerable disagreement in the literature over the nature of these correlations. Figure 5 shows the L_X- relationship for all the groups observed by the ROSAT PSPC in pointed-mode and a sample of clusters observed with various X-ray telescopes (Wu et al 1999). The solid line shows the best-fit relationship Wu et al (1999) derived from the cluster sample alone. Figure 5 shows that for the most part, groups are consistent with the cluster relationship, although there is considerable scatter particularly among the lowest luminosity groups. This conclusion was reached by Mulchaey & Zabludoff (1998), who found that a single relationship fit their sample of groups and rich clusters. Ponman et al (1996), Helsdon & Ponman (2000) also found that the L_X- for groups was basically consistent with the cluster relationship, although both studies noted that the relationship may become somewhat flatter for low velocity dispersion systems. (Within the errors, the slopes derived by Mulchaey & Zabludoff (1998), Ponman et al (1996), Helsdon & Ponman (2000) are indistinguishable; L_X ^4.3, ^4.9 and ^4.5, respectively). Therefore, there is fairly good agreement among the ROSAT studies based on pointed-mode data. However, Mahdavi et al (1997) derived a significantly flatter slope from their ROSAT All Sky Survey data (L_X ^1.56) and suggested that for low velocity dispersion systems the X-ray emission is dominated by hot gas clumped around individual galaxies. More recently, Mahdavi et al (2000) presented X-ray luminosities for a much larger sample of loose groups. In agreement with their earlier result, they find a much flatter L_X- for groups than for rich clusters. Mahdavi et al (2000) modeled the L_X- relationship as a broken power law, with a very flat slope (L_X ^0.37) for systems with velocity dispersion less than 340 km s^-1 and a cluster-like value (L_X ^4.0) for higher velocity dispersion systems. However, a visual inspection of Mahdavi et al's (2000) L_X- relationship (see Figure 4 of their paper) reveals that the need for a broken power law fit is driven by the one or two lowest velocity dispersion groups (out of a total sample of 61 detected groups.) Furthermore, nearly all the L_X upper limits derived by Mahdavi et al (2000) fall below their broken power law relationship (and therefore require a "steeper" relationship). Thus, the case for deviations from the L_X- cluster relationship is far from compelling. It is also worth noting that the velocity dispersions of the groups that appear to deviate the most from the cluster relationship are often based on very few velocity measurements (for example the most "deviant" system in Figures 4 and 5 has a velocity dispersion based on only four velocity measurements.) Zabludoff & Mulchaey (1998) have found that when velocity dispersions are calculated for X-ray groups from a large number of galaxies, as opposed to just the four or five brightest galaxies, the velocity dispersion is often significantly underestimated. Therefore, more detailed velocity studies of low velocity dispersion groups could prove valuable in verifying deviations from the cluster L_X- relation.

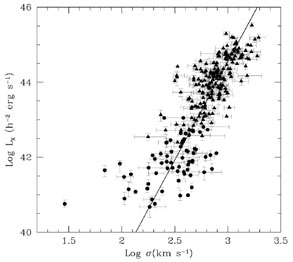Figure 5. Logarithm of optical velocity dispersion versus logarithm of X-ray luminosity for a sample of groups (circles) and clusters (triangles). The data are taken from the same sources cited in Figure 4. The solid line represents the best-fit found by Wu et al (1999) for the clusters sample (using an orthogonal distance regression method).

There is also considerable disagreement in the literature about the relationship between X-ray luminosity and gas temperature. Mulchaey & Zabludoff (1998) found that a single L_X-T relationship could describe groups and clusters (L_X T^2.8). However, both Ponman et al (1996), Helsdon & Ponman (2000) found much steeper relationships for groups (L_X T^8.2 and L_X T^4.9, respectively). These differences might be attributed to the different temperature ranges included in the studies. Mulchaey & Zabludoff's (1998) sample was largely restricted to hot groups (i.e. ~ 1 keV), whereas Ponman and collaborators have included much cooler systems (down to ~ 0.3 keV). Indeed, Helsdon & Ponman (2000) found that the steepening of the L_X-T relationship appears to occur below about 1 keV. Figure 6 suggests that the deviation of the cool groups from the cluster relationship is indeed significant. The fact that the L_X- relationship for groups appears to be similar to the relationship found for clusters, while the relationships involving gas temperature significantly depart from the cluster trends, may be an indication that non-gravitational heating is important in groups (Ponman et al 1996, Helsdon & Ponman 2000). However, the group X-ray luminosities may be biased somewhat low because groups are detected to a smaller fraction of their virial radius than richer systems, and if comparisons are made at the same mass over-density level, groups would likely fall closer to the cluster relation.

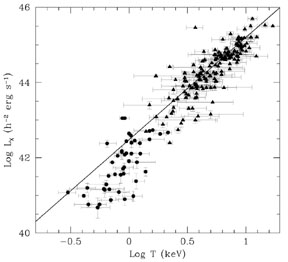Figure 6. Logarithm of the X-ray temperature versus logarithm of X-ray luminosity for a sample of groups (circles) and clusters (triangles). The data are taken from the same sources cited in Figure 4. The solid line represents the best-fit found by Wu et al (1999) for the clusters sample (using an orthogonal distance regression method). The observed relationship for groups is somewhat steeper than the best-fit cluster relationship.