7.3. Characteristic scales

The current data are contrasted with some CDM models in figure 17. The key feature that is picked out is the peak at 220, together with harmonics of this scale at higher . Beyond 1000, the spectrum is clearly damped, in a manner consistent with the expected effects of photons diffusing away from baryons (Silk damping), plus smearing of modes with wavelength comparable to the thickness of the last-scattering shell. This last effect arises because recombination is not instantaneous, so the redshift of last scattering shows a scatter around the mean, with a thickness corresponding to approximately _r = 7(_m h²)^-1/2 Mpc. On scales larger than this, we see essentially an instantaneous imprint of the pattern of potential perturbations and the acoustic baryon/photon oscillations.

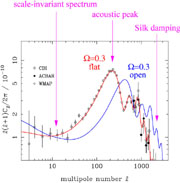Figure 17. Angular power spectra 2() = ( + 1)C / 2 for the CMB, plotted against angular wavenumber in radians-1. For references to the experimental data, see Spergel et al. (2003), Kuo et al. (2002) and Pearson et al. (2002). The two lines show model predictions for adiabatic scale-invariant CDM fluctuations, calculated using the CMBFAST package (Seljak & Zaldarriaga 1996). These have (n, m, b, h) = (1, 0.3, 0.05, 0.65) and have respectively v = 1 - m (`flat') and v = 0 (`open'). The main effect is that open models shift the peaks to the right, as discussed in the text.

The significance of the main acoustic peak scale is that it picks out the (sound) horizon at last scattering. The redshift of last scattering is almost independent of cosmological parameters at z_LS 1100, although a more precise approximation is given in Appendix C of Hu & Sugiyama (1995). If we assume that the universe is matter dominated at last scattering, the horizon size is

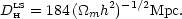(145)

The angle this subtends is given by dividing by the current size of the horizon (strictly, the comoving angular-diameter distance to z_LS). Again, for a matter-dominated model, this is

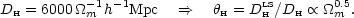(146)

This expression lies behind the common statement that the CMB data require a flat universe. Figure 17 shows that heavily open universes yield a main CMB peak at scales much smaller than the observed 220, and these can be ruled out. Indeed, open models were disfavoured for this reason long before any useful data existed near the peak, simply because of strict upper limits at 1500 (Bond & Efstathiou 1984). However, once a non-zero vacuum energy is allowed, the story becomes more complicated, and it turns out that large degrees of spatial curvature cannot be excluded using the CMB alone.