8. MODEL DEGENERACIES INHERENT IN CMB DATA

8.1. Geometrical degeneracy

The normal argument for flatness from the CMB starts with the comoving horizon size at last scattering

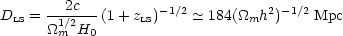(147)

and divides it by the present-day horizon size for a zero- universe,

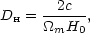(148)

to yield a main characteristic angle that scales as _m^1/2. Large curvature (i.e. low _m) is ruled out because the main peak in the CMB power spectrum is not seen at very small angles. However, introducing vacuum energy changes the conclusion. If we take a family of models with fixed initial perturbation spectra, fixed physical densities _{m m} h², _{b b} h², it is possible to vary both _v and the curvature to keep a fixed value of the angular size distance to last scattering, so that the resulting CMB power spectra are identical. This degeneracy was analyzed comprehensively by Efstathiou & Bond (1999), and we now summarize the main results.

The usual expression for the comoving angular-diameter distance is

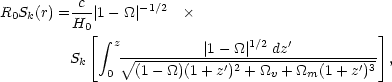(149)

where = _m + _v. Defining _{i i} h², this can be rewritten in a way that has no explicit h dependence:

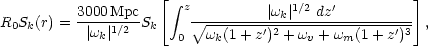(150)

where _k (1 - _m - _v)h². This parameter describes the curvature of the universe, treating it effectively as a physical density that scales as a^-2. This is convenient for the present formalism, but it is important to appreciate that curvature differs fundamentally from a hypothetical fluid with such an equation of state.

The sound horizon distance at last scattering is governed by the relevant physical densities, _m and _b; if _m and _b are given, the shape of the spatial power spectrum is determined. The translation of this into an angular spectrum depends on the angular-diameter distance, which is a function of these parameters, plus _k and _v. Models in which _m^1/2 R₀ S_k(r) is a constant have the same angular horizon size. For fixed _m and _b, there is therefore a degeneracy between curvature (_k) and vacuum (_v): these two parameters can be varied simultaneously to keep the same apparent distance, as illustrated in figure 19.

Figure 19. The geometrical degeneracy in the CMB means that models with fixed m h2 and b h2 can be made to look identical by varying the curvature against vacuum energy, while also varying the Hubble parameter. This degeneracy is illustrated here for the case m m h2 = 0.2. Models along a given line are equivalent from a CMB point of view; corresponding lines in the upper and lower panels have the same line style. Note that supplying external information about h breaks the degeneracy. This figure assumes scalar fluctuations only; allowing tensor modes introduces additional degeneracies - mainly between the tensor fraction and tilt.

In short, this degeneracy occurs because the physical densities control the structure of the perturbations in physical Mpc at last scattering, while curvature, _v and _m govern the proportionality between length at last scattering and observed angle. The degeneracy is not exact, and is weakly broken by the Integrated Sachs-Wolfe effect from evolving potentials at very low multipoles, and second-order effects at high . However, strong breaking of the degeneracy requires additional information. This could be in the form of external data on the Hubble constant, which obeys the relation

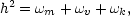(151)

so specifying h in addition to the physical matter density fixes _v + _k and removes the degeneracy. A more elegant approach is to add results from large-scale structure, so that conclusions are based only on the shapes of power spectra. Efstathiou et al. (2002) show that doing this yields a total density (| - 1| < 0.05) at 95% confidence.