6.3. The flux-redshift test: Supernovae Ia

Type I supernovae are thought to be nuclear explosions of carbon/oxygen white dwarfs in binary systems. The white dwarf (a stellar remnant supported by the degenerate pressure of electrons) accretes matter from an evolving companion and its mass increases toward the Chandrasekhar limit of about 1.4 M (this is the mass above which the degenerate electrons become relativistic and the white dwarf unstable). Near this limit there is a nuclear detonation in the core in which carbon (or oxygen) is converted to iron. A nuclear flame propagates to the exterior and blows the white dwarf apart (there are alternative models but this is the favored scenario [45]).

These events are seen in both young and old stellar populations; for example, they are observed in the spiral arms of spiral galaxies where there is active star formation at present, as well as in elliptical galaxies where vigorous star formation apparently ceased many Gyr ago. Locally, there appears to be no difference in the properties of SNIa arising in these two different populations, which is important because at large redshift the stellar population is certainly younger.

The peak luminosity of SNIa is about 10¹⁰ L which is comparable to that of a galaxy. The characteristic decay time is about one month which, in the more distant objects, is seen to be stretched by 1+z as expected. The light curve has a characteristic form and the spectra contain no hydrogen lines, so given reasonable photometric and spectroscopic observations, they are easy to identify as SNIa as opposed to type II supernovae; these are thought to be explosions of young massive stars and have a much larger dispersion in peak luminosity [46].

The value of SNIa as cosmological probes arises from the high peak luminosity as well as the observational evidence (locally) that this peak luminosity is the sought-after standard candle. In fact, the absolute magnitude, at peak, varies by about 0.5 magnitudes which corresponds to a 50%-60% variation in luminosity; this, on the face of it, would make them fairly useless as standard candles. However, the peak luminosity appears to be well-correlated with decay time: the larger L_peak, the slower the decay. There are various ways of quantifying this effect [46], such as

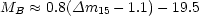(6.3)

where M_B is the peak absolute magnitude and m₁₅ is the observed change in apparent magnitude 15 days after the peak [47]. This is an empirical relationship, and there is no consensus about the theoretical explanation, but, when this correction is applied it appears that L_peak < 20%. If true, this means that SNIa are candles that are standard enough to distinguish between cosmological models at z 0.5.

In a given galaxy, supernovae are rare events (on a human time scale, that is), with one or two such explosions per century. But if thousands of galaxies can be surveyed on a regular and frequent basis, then it is possible to observe several events per year over a range of redshift. About 10 years ago two groups began such ambitious programs [48, 49]; the results have been fantastically fruitful and have led to a major paradigm shift.

The most recent results are summarized in [50]: at present, about 230 SNIa have been observed out to z = 1.2. The bottom line is that SNIa are 10% to 20% fainter at z 0.5 than would be expected in an empty (_tot = 0) non-accelerating Universe. But, significantly, at z 1 the supernovae appear to become brighter again relative to the non-accelerating case; this should happen in the concordance model at about this redshift because it is here that the cosmological constant term in the Friedmann equation (eq. 3.7 ) first begins to dominate over the matter term. This result is shown in Fig. 8 which is a plot of the median m, the observed deviation from the non-accelerating case, in various redshift bins as a function of redshift (i.e., the horizontal line at m = 0 corresponds to the empty universe). The solid curves show the prediction for various flat (_tot = 1) models with the value of the cosmological term indicated. It is evident that models dominated by a cosmological term or by matter are inconsistent with the observations at extremely high levels of significance, while the concordance model agrees quite well with the observations.

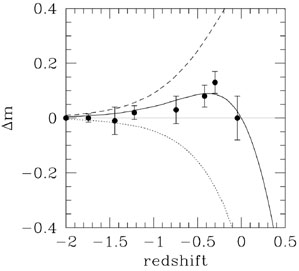Figure 8. The Hubble diagram for SNIa normalized to an empty non-accelerating Universe. The points are binned median values for 230 supernovae [50] The curves show the predictions for three flat (tot = 0) cosmological models: The dashed line is the model dominated by a cosmological constant ( = 0.9), the solid curve is the concordance model ( = 0.7), and the dotted curve is the matter dominated model ( = 0.1).

It is also evident from the figure that the significance of the effect is not large, perhaps 3 or 4 (quite a low level of significance on which to base a paradigm shift). When all the observed supernovae are included on this plot, it is quite a messy looking scatter with a minimum ² per degree of freedom (for flat models) which is greater than one. Moreover the positive result depends entirely upon the empirical peak luminosity-decay rate relationship and, of course, upon the assumption that this relation does not evolve. So, before we become too enthusiastic we must think about possible systematic effects and how these might affect the conclusions. These effects include:

1) Dust: It might be that supernovae in distant galaxies are more (or less) dimmed by dust than local supernovae. But normal dust, with particle sizes comparable to the wavelength of light, not only dims but also reddens (for the same reason, Rayleigh scattering, that sunsets are red). This is quantified by the so-called color excess. Remember I said that astronomers measure the color of an object by its B-V color index (the logarithm of a flux ratio). The color excess is defined as

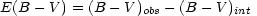(6.4)

where obs means the observed color index and int means the intrinsic color index (the color the object would have with no reddening). In our own galaxy it is empirically the case that the magnitudes of absorption is proportional to this color excess, i.e.,

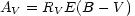(6.5)

where R_V is roughly constant and depends upon average grain properties. So assuming that the dust in distant galaxies is similar to the dust in our own, it should be possible to estimate and correct for the dust obscuration. Significantly [48], it appears that there is no difference between E(B-V) for local and distant supernovae. This implies that the distant events are not more or less obscured than the local ones.

2) Grey dust: It is conceivable (but unlikely) that intergalactic space contains dust particles which are significantly larger than the wavelength of light. Such particles would dim but not redden the distant supernovae and so would be undetectable by the method described above [51]. It is here that the very high redshift supernovae (z > 1) play an important role. If this is the cause of the apparent dimming we might expect that the supernovae would not become brighter again at higher redshift.

3) Evolution: It is possible that the properties of these events may have evolved with cosmic time. As I mentioned above, the SN exploding at high redshift come from a systematically younger stellar population than the objects observed locally. Moreover, the abundance of metals was smaller in the earlier Universe than now; this evolving composition, by changing the opacity in the outer layers or the composition of the fuel itself could lead to a systematic evolution in peak luminosity. Here it is important to look for observational differences between local and distant supernovae, and there seem to be no significant differences in most respects, the spectrum or the light curve. There is, however, a suggestion that distant supernovae are intrinsically bluer than nearby objects [46]. If this effect is verified, then it could not only point to a systematic difference in the objects themselves, but could also have lead to an underestimate of the degree of reddening in the distant SN. It is difficult, in general, to eliminate the possibility that the events themselves were different in the past and that this could mimic the effect of a cosmological constant [52]; a deeper theoretical understanding of the SNIa process is required in order to realistically access this possibility.

4) Sample evolution: The sample of SN selected at large redshift may differ from the nearby sample that is used, for example, to calibrate the peak luminosity-decline rate correlation. There does appear to be an absence, at large redshift, of SN with very slowly declining light curves - which is to say, very luminous SN that are seen locally. Perhaps a class of more luminous objects is missing in the more distant Universe due to the fact that these SN emerge from a systematically younger stellar population. One would hope that the luminosity-decline rate correlation would correct for this effect, assuming, of course, that this relation itself does not evolve.

5) Selection biases: There is a dispersion in the luminosity-decline rate relationship, and in a flux-limited sample, one tends to select the higher luminosity objects. Astronomers call this sort of bias the "Malmquist effect" and it is always present in such observational data. Naively, one would expect such a bias to lead to an underestimate of the true luminosity, and, therefore an underestimate luminosity distance; the bias actually diminishes the apparent acceleration. But there is another effect which is more difficult to access: The most distant supernovae are being observed in the UV of their own rest frame. SNIa are highly non-uniform in the UV, and K-corrections are uncertain. This could introduce systematic errors at the level of a few hundredths of a magnitudes [50].

We see that there are a number of systematic effects that could bias these results. A maximum likelihood analysis over the entire sample [50], confirms earlier results that the confidence contours in _m - space are stretched along a line = 1.4_m + 0.35 and that the actual best fit is provided by a model with _m 0.7 and 1.3 - not the concordance model. Of course, if we add the condition that _tot = 1 (a flat Universe) then the preferred model becomes the concordance model. In [50] it is suggested that this apparent deviation is due to the appearance of one or more of the systematic effects discussed above near z = 1 at the level of 0.04 magnitudes.

The result that SNIa are systematically dimmer near z = 0.5 than expected in a non-accelerating Universe is robust. At the very least it can be claimed with reasonable certainty that the Universe is not decelerating at present. However, given the probable presence of systematic uncertainties at the level of a few hundredths of a magnitude, it is difficult to constrain the equation of state (w) of the dark energy or its evolution (dw / dt) until these effects are better understood. I will just mention that lines of constant age, t_o H_o, are almost parallel to the best fit line in the _m - plane mentioned above. This then gives a fairly tight constraint on the age in Hubble times [50]; i.e. t_o H_o = 0.96 ± 0.4, which is consistent with the WMAP result. In a near flat Universe this rules out the dominance of matter and requires a dark energy term.