


The driving force behind starburst-driven winds is the mechanical
energy from stellar winds and supernova events (e.g.,
Chevalier & Clegg
1985).
This mechanical energy is quickly thermalized to produce
a hot cavity with a temperature ~ 108
 -1 K, where
-1 K, where
 =
Mtotal / Mejecta
=
Mtotal / Mejecta
 1 is the
mass-loading term. This over-pressured cavity expands through the
ambient medium, sweeping this material up in the process to produce a
bubble-like structure. The complex interaction between the wind and
the ISM of the host galaxy has been the subject of several numerical
simulations (e.g.,
MacLow & McCray
1988;
Suchkov et al. 1994,
1996;
MacLow & Ferrara
1999;
D'Ercole & Brighenti
1999;
Strickland & Stevens
2000;
Silich &
Tenorio-Tagle 2001).
If radiative energy
losses are negligible (probably a good assumption in some objects; e.g.,
Heckman et al. 2001),
the bubble expands adiabatically through
the galaxy ISM with a velocity ~ 100 n0-0.2
1 is the
mass-loading term. This over-pressured cavity expands through the
ambient medium, sweeping this material up in the process to produce a
bubble-like structure. The complex interaction between the wind and
the ISM of the host galaxy has been the subject of several numerical
simulations (e.g.,
MacLow & McCray
1988;
Suchkov et al. 1994,
1996;
MacLow & Ferrara
1999;
D'Ercole & Brighenti
1999;
Strickland & Stevens
2000;
Silich &
Tenorio-Tagle 2001).
If radiative energy
losses are negligible (probably a good assumption in some objects; e.g.,
Heckman et al. 2001),
the bubble expands adiabatically through
the galaxy ISM with a velocity ~ 100 n0-0.2
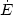 420.2
t7-0.4 km s-1, where
n0 is the ambient nucleon density in cm-3,
420.2
t7-0.4 km s-1, where
n0 is the ambient nucleon density in cm-3,
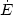 42 is
the rate of deposition of mechanical energy in 1042 erg
s-1, and t7 is the age of the bubble in
107 years (e.g.,
Weaver et al. 1977).
42 is
the rate of deposition of mechanical energy in 1042 erg
s-1, and t7 is the age of the bubble in
107 years (e.g.,
Weaver et al. 1977).
A powerful starburst may inject enough energy to produce a cavity of
hot gas that can burst out of the disk ISM,
at which point the dense walls of the bubble start accelerating
outward, become Rayleigh-Taylor unstable, and break up into cloudlets
and filaments. If halo drag is negligible (probably not a good
assumption in general), the wind fluid may reach terminal velocities
as high as ~ 3000
A critical quantity in all of these calculations is the thermalization
efficiency, or the percentage of the mechanical energy from the
starburst that goes into heating the gas. Unfortunately, this
quantity is poorly constrained observationally. Most simulations
assume a thermalization efficiency of 100%, i.e. none of the energy
injected by the starburst is radiated away. In reality, this
efficiency depends critically on the environment, and is likely to be
significantly less than 100% in the high-density environment of
powerful nuclear starbursts (e.g.,
Thornton et al. 1998;
Strickland & Stevens
2000;
Silich, Tenorio-Tagle,
& Muñoz-Tuñón 2003).
Galactic magnetic fields may also "cushion" the effects of the
starburst on the ISM, and reduce the impact of the galactic wind on
the host galaxy and its environment (e.g.,
Tomisaka 1990;
Ferrière et
al. 1991;
Slavin & Cox 1992;
Mineshinge et al. 1993;
Ferrière 1998).
 -1 km
s-1, well in excess of
the escape velocity of the host galaxy. In contrast, the terminal
velocities of clouds accelerated by the wind are more modest, of order
~ 600
-1 km
s-1, well in excess of
the escape velocity of the host galaxy. In contrast, the terminal
velocities of clouds accelerated by the wind are more modest, of order
~ 600 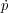 340.5
340.5
 w-0.5 r0, kpc
Ncloud, 21-0.5, where
w-0.5 r0, kpc
Ncloud, 21-0.5, where
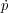 34 is the
wind momentum flux in 1034 dynes,
34 is the
wind momentum flux in 1034 dynes,
 W is the
solid angle of the wind in steradians,
r0, kpc is the initial position of the cloud in
kpc, and Ncloud, 21 is the column density of the cloud in
1021 cm-2
(Strel'nitskii &
Sunyaev 1973;
Heckman et al. 2000).
W is the
solid angle of the wind in steradians,
r0, kpc is the initial position of the cloud in
kpc, and Ncloud, 21 is the column density of the cloud in
1021 cm-2
(Strel'nitskii &
Sunyaev 1973;
Heckman et al. 2000).