15.5.2. Evolutionary Models of Radio Luminosity Functions

Ryle and Clarke (1961) showed that their 178-MHz source count above S = 0.25 Jy is incompatible with nonevolving Einstein-de Sitter and steady-state models. They also recognized that "the introduction of evolutionary effects which appear to be necessary will make the selection of a unique [world] model difficult." In a paper introducing many of the features found in subsequent model calculations, Longair (1966) modeled the 178-MHz source count, strong-source luminosity distribution, and integrated emission from discrete sources in an evolving Einstein-de Sitter universe. "Power-law" evolution proportional to (1 + z)ⁿ yielded satisfactory fits only if restricted to the most luminous sources and truncated at high redshifts. "Exponential" evolution proportional to e^-t/, where t is the cosmic time and the evolutionary time scale, was proposed by Rowan-Robinson (1970) because it does not diverge at high redshifts. Although this parametric form shows that the data do not require a real truncation of evolution at large z, Rowan-Robinson also considered physical factors that must ultimately truncate evolution, such as the time needed to form the parent galaxies of radio sources and electron energy losses by inverse Compton scattering off the microwave background radiation. A parametric model explicitly constrained by astrophysical assumptions was tried by Grueff and Vigotti (1977) to explain the 408-MHz source count and the luminosity distributions of sources stronger than S = 10 Jy and S = 0.9 Jy. They assumed that quasars form at z = 2.5 and evolve into galaxies whose radio-emitting lifetimes are inversely proportional to their radio luminosities. One difficulty with this model is that the evolution of low-luminosity radio sources can be minimized only if their radio emitting lifetimes are comparable with the Hubble time.

Extensions of the source counts to lower flux densities and the availability of more complete redshift data for strong sources eventually justified reexamination of the first parametric models. Wall et al. (1980) found that the 408-MHz source count extending to S = 0.01 Jy and the "all-sky" luminosity distribution of sources stronger than S = 10 Jy were sufficient to show that "power law" models are a poor representation of the cosmological evolution of powerful radio sources. They also investigated "exponential" evolution of the form exp[M(1 - t / t₀)], where M specifies the strength of the evolution and t₀ is the present age of the universe. Successful models were constructed in which M depends on luminosity [e.g., M = 0 for L < L₁, M = M_max for L > L₂, and M = M_max(log L - log L₁) / (log L₂ - log L₁) for L₁ < L < L₂] or redshift. Robertson's (1978, 1980) "free-form" analysis of essentially the same data did not assume a functional form for the redshift dependence of evolution, but used the data to solve for it. However, these data cannot fully determine both the redshift and luminosity dependence of the evolution, so Robertson did assume a parametric form for the luminosity dependence that is similar to the one specified above. An artifact of the rather sharp changes of evolution with luminosity implied by this parametric form is a markedly bimodal redshift distribution at low flux densities (cf. Figure 10 of Wall et al. 1980).

The preceding models approximate the spectral-index distributions of all sources by a single -function centered on 0.8, and they work well for data selected at any one low ( < 1 GHz) frequency. Extensive sky surveys made at 2.7 and 5 GHz in the late 1960s revealed significant populations of sources with 0 and led to models accounting for both the steep- and flat-spectrum sources simultaneously (Schmidt 1972, Fanaroff and Longair 1973, Petrosian and Dickey 1973). The decline in the fraction of flat-spectrum sources as the 5-GHz sample flux-density limit is decreased below S 1 Jy (Figure 15.6) can be reproduced if (1) the local spectral luminosity function is separated or "factorized" into independent spectral-index and luminosity functions at some frequency of lower than 5 GHz and (2) the rate of evolution is the same for both steep- and flat-spectrum sources. Then there is an inverse correlation induced between a and L at higher frequencies, and the weighted 5-GHz count of flat-spectrum sources peaks at a higher flux density than the weighted count of steep-spectrum sources.

There have been some indications that flat-spectrum quasars may evolve less than steep-spectrum or optically selected quasars. The weighted count of flat-spectrum sources (mostly quasars) peaks near S 1 Jy (Figure 15.6), so the average count slope is nearly Euclidean for the flat-spectrum sources found in the first large-scale 5-GHz surveys that are complete down to S 0.6 Jy. Because the source count slope and <V / V_m> (< ahref="Condon4.html#4.1">Section 15.4.1) are closely related (Longair and Scheuer 1970), quasar identifications of flat-spectrum sources from these surveys have nearly static-Euclidean values <V / V_m> 0.5 (Schmidt 1976), much lower than the <V / V_m> 0.7 of quasars identified with primarily steep-spectrum 3CR quasars stronger than S = 9 Jy at = 178 MHz (Schmidt 1968). While high <V / V_m> values indicate evolution, <V / V_m> 0.5 does not exclude evolution because the distribution of <V / V_m> may still be nonuniform. Evolution increasing at low redshifts (z < 2, for example) and decreasing at higher redshifts still in the sample volumes V_m could yield a nonuniform V / V_m distribution with <V / V_m> 0.5. Just this situation is probably occurring. The 3CR quasars can be seen only out to limiting redshifts z_m 2, and their large <V / V_m> value reflects monotonically increasing evolution up to z 2; flat-spectrum quasars stronger than S = 0.6 Jy can be seen at higher redshifts (z_m 3 or 4) where their evolution has started to decline. Kulkarni (1978) produced models that allow the steep- and flat-spectrum populations to evolve independently, approximate the spectral-index distributions of each population by Gaussians, and include the correlation of with L among steep-spectrum sources. In both the Kulkarni (1978) and Machalski (1981) models, the flat- and steep-spectrum sources evolve differently, but later models by Peacock and Gull (1981) and Condon (1984b) show that these two spectral classes may indeed evolve at the same rates without violating the data constraints.

Condon (1984b) searched for a single model to fit in detail a wide range of available radio data (the local luminosity functions of spiral and elliptical galaxies at = 1.4 GHz; source counts at = 0.408, 0.61, 1.4, 2.7, and 5 GHz; counts of steep- and flat-spectrum sources at = 2.7 and 5 GHz; spectral-index distributions of sources in a number of samples complete to different flux-density limits at = 1.4, 2.7, and 5 GHz; redshift/spectral-index diagrams and redshift distributions of strong sources selected at 1.4, 2.7, and 5 GHz). The local 1:4-GHz visibility functions of spiral and elliptical galaxies were approximated by hyperbolas [< ahref="Condon4.html#Figure 3">Figure 15.3(b)]. The spectral luminosity function was "factorized" at v_f = 1.4 GHz. The spectral-index function was approximated by two Gaussians, and the median spectral index of the steep-spectrum Gaussian varied with log(z). The evolution was constrained by the assumption that the form of the = 1.4 GHz luminosity function be independent of redshift:

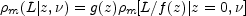(15.29)

where f (z) and g(z) are "free-form" functions that describe "luminosity evolution" and "density evolution," respectively. This "translation evolution" [so named because the evolution can be represented by translating the local luminosity function in the (log L, log_m)-plane] could result from evolutionary mechanisms that do not discriminate on the basis of source luminosity. A simple model was found that fits the radio data (curves in Figures 15.3, 15.5 - 15.9) as well as predicting redshift distributions (Figure 15.10) consistent with the magnitude distributions of faint-source identifications. Large values of the evolution function E(L, z) (Figure 15.11) are restricted to high luminosities, as they must be to avoid producing too many faint sources. The luminosity range in which E(L, z) is large is not a free parameter in this model; it is determined by the location of the bend near L 10²⁵ W Hz^-1 in the local luminosity function [Figure 15.3(a)]. Since this model assumes that all sources evolve equally, it demonstrates by example that restricting large E(L, z) values to high luminosities does not imply that "only powerful sources evolve." Such an overinterpretation of the evolution function has led, for example, to the incorrect belief that only the (relatively luminous) radio quasars evolve, but that the (less luminous) radio galaxies do not.

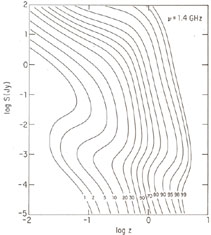Figure 15.10. Model redshift distributions at = 1.4 GHz (From Condon 1984b). Abscissa: log redshift. Ordinate: log flux density (Jy). Parameter: percentage of sources at flux density S with redshifts less than z.

All of the models described above are based on strong assumptions about the form of evolution in the (L, z)-plane. They show that evolutionary forms consistent with the data exist, but these solutions are certainly not unique. In order to explore the range of luminosity functions consistent with the source counts at = 0.408, 2.7, and 5 GHz, luminosity distributions, and optical identification data, Peacock and Gull (1981) generated a number of "free-form" models in which the evolution is described by power series in log(L) and either log(1 + z) or log(1 - t / t₀) so that it is "free-form" in both luminosity and time, at least to the extent that evolution varies smoothly with these quantities. The possibility of a sharp cutoff at high z was also considered. Steep- and flat-spectrum sources were allowed to evolve independently, and their spectral-index distributions were approximated by -functions. This approximation affects theaccuracy with which the model can reproduce the radio data (Condon 1984b) but does not significantly increase the uncertainty of the derived evolving luminosity functions (Peacock 1985). Their successful models indicate that flat- and steep-spectrum sources evolve similarly, with only the most luminous sources exhibiting large changes in their comoving density with epoch. However, the density of sources in most areas of the (L, z)-plane is not well defined by the data. By locating the areas of greatest uncertainty, Peacock and Gull could specify the most important data still needed - source counts and redshift distributions of faint flat-spectrum sources in particular. The redshifts of forty-one flat-spectrum quasars with S 0.5 Jy at = 2.7 GHz were later added to the Peacock and Gull (1981) data base, and they allowed Peacock (1985) to suggest that the density of powerful flat-spectrum sources declines between z 2 and z 4 (unless the small number of quasars still lacking spectroscopic redshifts all have z > 3).

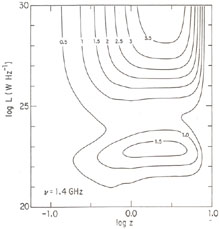Figure 15.11. Contour plot of the Condon (1984b) model evolution function at = 1.4 GHz. Abscissa: log redshift. Ordinate: log luminosity (W Hz-1). Contours: log evolution function.