


ABUNDANCES FROM EMISSION-LINE OBJECTS
We present here only a brief overview of abundance determining methods relevant to emission-line objects. A list of prominent nebular emission lines is presented in Table A1, where we provide the ion, wavelength, and dominant excitation mechanism for each line. Readers interested in greater detail are urged to consult information in Spitzer (1978), Aller (1984), Osterbrock (1988, 1989), and Williams & Livio (1995). The atomic data used for the abundance calculations are reviewed by Butler (1993).
a
Excitation mechanism, where C = collisional, R = recombination.
The basic method for obtaining the abundance of an element in
emission-line objects comprises two steps: (1) determine abundances of
the ions of that element whose emission lines are directly observable,
and (2) adjust the total of the ionic abundances by a factor which
accounts for ions of the same element which are unobservable.
Consider step 1. An ionic abundance relative to H+ is related
to the observed strength of an emission line integrated over wavelength,
corrected for interstellar reddening, and expressed relative to the
H
where Ni, NH++, and
Ne are local number densities of the ion giving
rise to the line
Adding the observed ionic abundances for an element together gives us a
subtotal which differs from the desired total by the abundances of the
ions whose emission lines are not observed. Thus, in step 2 above we
determine an ionization correction factor, ICF(X), for element X by
which we multiply the subtotal to produce the total elemental abundance
relative to H+. Mathematically, the number density of an
element NX / NH can be expressed as
Ionization correction factors may be inferred from model simulations of
nebulae or estimated by assuming that ions with similar ionization
potentials are present in the gas in similar ratios to their total
abundances. Thus, because the ionization potentials of O+2
and He+ are 54.9 and 54.4 ev, respectively, the total
abundance of unobservable (in the optical) higher ionization stages such
as O+3 and beyond with respect to total O is similar to
relative amounts of He+2, an optically observable ion, with
respect to total He. A good compilation and discussion of a broad range
of ICFs may be found in the appendix of
Kingsburgh & Barlow (1994).
Additionally, model grids such as those by
Stasinska & Schaerer (1997)
may be used to derive ICFs for a nebula assuming the central star
temperature is known.
The above method breaks down most frequently for metal-rich nebulae with
low equilibrium temperatures, in which case auroral lines such as
[O III]
Finally, the accuracy of abundances in emission-line systems is
threatened by the proposed existence of small-scale temperature
fluctuations along the line of sight, first described by
Peimbert (1967).
In this picture, an electron temperature measured with forbidden lines
is actually overestimated when fluctuations are present but
ignored. This in turn causes an underestimation of an abundance ratio
such as O+2/H+ when it's based upon a
forbidden/permitted line ratio such as [O III]
Ion
Wavelength (Å)
Excitation a
Ion
Wavelength (Å)
Excitation
C IV
1549
C
H I
4861
R
He II
1640
R
[O III]
4959,5007
C
C III]
1909
C
[N II]
5199
C
[OII]
3727
C
HeI
5876
R
[NeIII]
3869, 3968
C
[OI]
6300, 6360
C
HeI
3889
R
[SIII]
6312
C
[SII]
4072
C
[NII]
6548, 6584
C
HI
4101
R
HI
6563
R
HI
4340
R
[SII]
6716, 6731
C
[OIII]
4363
C
[ArIII]
7135
C
HeI
4471
R
[OII]
7325
C
HeII
4686
R
[SIII]
9069, 9532
C
 strength,
I
strength,
I /
IH
/
IH , through the respective reaction rate coefficients,
, through the respective reaction rate coefficients,

 and
and
 H
H in ergs
cm3 s-1 sr-1, such that
in ergs
cm3 s-1 sr-1, such that
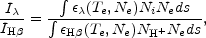
(A1)
 , H+, and
electrons, respectively. The integrals arise because local products are
integrated along the line of sight. Note that the rates are functions of
the local electron temperature (Te) and density
(Ne), although a good simplifying assumption is
that these are constant within the nebular regions actually dominated by
the ions in question. Te is usually determined
using the line strength ratio of two lines such as [O III]
, H+, and
electrons, respectively. The integrals arise because local products are
integrated along the line of sight. Note that the rates are functions of
the local electron temperature (Te) and density
(Ne), although a good simplifying assumption is
that these are constant within the nebular regions actually dominated by
the ions in question. Te is usually determined
using the line strength ratio of two lines such as [O III]
 4363 and
4363 and
 5007 whose upper
energy levels are relatively far apart. Ne is derived
from the ratio of two lines such as [S II]
5007 whose upper
energy levels are relatively far apart. Ne is derived
from the ratio of two lines such as [S II]

 6716, 6731 whose upper
energy levels are closely spaced but the transitions differ
significantly in their sensitivities to collisional deexcitation.
6716, 6731 whose upper
energy levels are closely spaced but the transitions differ
significantly in their sensitivities to collisional deexcitation.
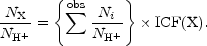
(A2)
 4363 are too weak to
measure, and thus the temperature cannot be determined. One way around
the problem is to calculate a detailed photoionization model of the
nebula using input abundances and other physical parameters which
produce an output set of line strengths closely matching the observed
ones. Actual abundances are then inferred from the model input. A
simpler solution is the "strong-line method," which uses a composite of
strong, observable emission line strengths whose value tracks an
abundance ratio. The most significant example is R23
4363 are too weak to
measure, and thus the temperature cannot be determined. One way around
the problem is to calculate a detailed photoionization model of the
nebula using input abundances and other physical parameters which
produce an output set of line strengths closely matching the observed
ones. Actual abundances are then inferred from the model input. A
simpler solution is the "strong-line method," which uses a composite of
strong, observable emission line strengths whose value tracks an
abundance ratio. The most significant example is R23
 ([O III] + [O II])
/ H
([O III] + [O II])
/ H , first
introduced by
Pagel et al. (1979),
which comprises the sum of [O III] and [O II] nebular line strengths relative to the strength of
H
, first
introduced by
Pagel et al. (1979),
which comprises the sum of [O III] and [O II] nebular line strengths relative to the strength of
H and is
related in a complicated but understandable way to the total oxygen
abundance O/H. This method has been refined and discussed more recently
by
Edmunds & Pagel (1984),
Edmunds (1989), and
McGaugh (1991),
and of course it is not problem-free. Because the metal-rich portion of
this relation must currently be calibrated with models, uncertainties
arise from parameter choices such as relative depletion
(Henry 1993;
Shields & Kennicutt 1995)
and gas density
(Oey & Kennicutt 1993).
Finally, analogous methods for obtaining N/O and S/O are presented by
Thurston, Edmunds, & Henry (1996)
and Díaz (1999), respectively.
and is
related in a complicated but understandable way to the total oxygen
abundance O/H. This method has been refined and discussed more recently
by
Edmunds & Pagel (1984),
Edmunds (1989), and
McGaugh (1991),
and of course it is not problem-free. Because the metal-rich portion of
this relation must currently be calibrated with models, uncertainties
arise from parameter choices such as relative depletion
(Henry 1993;
Shields & Kennicutt 1995)
and gas density
(Oey & Kennicutt 1993).
Finally, analogous methods for obtaining N/O and S/O are presented by
Thurston, Edmunds, & Henry (1996)
and Díaz (1999), respectively.
 5007 /
H
5007 /
H . When
ratios of permitted lines are used the effect is minimal and so
abundances inferred from permitted/permitted line ratios are unaffected
and systematically higher than abundances from forbidden/permitted
ratios. Temperature fluctuations have been used to explain, among many
other things, the significant discrepancy in planetary nebula carbon
abundances
(Peimbert, Torres-Peimbert, &
Luridiana 1995),
where those determined using C II
. When
ratios of permitted lines are used the effect is minimal and so
abundances inferred from permitted/permitted line ratios are unaffected
and systematically higher than abundances from forbidden/permitted
ratios. Temperature fluctuations have been used to explain, among many
other things, the significant discrepancy in planetary nebula carbon
abundances
(Peimbert, Torres-Peimbert, &
Luridiana 1995),
where those determined using C II
 4267 /
H
4267 /
H , say, are
often several times greater than abundances inferred from C III]
, say, are
often several times greater than abundances inferred from C III]
 1909 /
H
1909 /
H .
Esteban et al. (1998)
found the effect to be small in the Orion Nebula, while
Liu (1998)
found a large effect in the planetary nebula NGC 4361, although it was
insufficient for explaining the discrepancy between carbon abundances
from recombination and collisionally excited lines. The issue of
temperature fluctuations is an important one, albeit unresolved. Further
details can be found in
Peimbert (1995),
Mathis, Torres-Peimbert, & Peimbert
(1998), and
Stasinska (1998).
.
Esteban et al. (1998)
found the effect to be small in the Orion Nebula, while
Liu (1998)
found a large effect in the planetary nebula NGC 4361, although it was
insufficient for explaining the discrepancy between carbon abundances
from recombination and collisionally excited lines. The issue of
temperature fluctuations is an important one, albeit unresolved. Further
details can be found in
Peimbert (1995),
Mathis, Torres-Peimbert, & Peimbert
(1998), and
Stasinska (1998).