


The Law of Nebular Distribution when Red-Shifts are not interpreted as Velocity-Shifts
We can now formulate the law of nebular distribution on the assumption that the nebulae are not rapidly receding. 3 The energy-corrections corresponding to red-shifts at the limits of the various surveys exactly compensate for the apparent thinning out in the World Picture. Numbers of nebulae are strictly proportional to the volumes of space they occupy. If the universe is not rapidly expanding, the observable region is thoroughly homogeneous out as far as accurate surveys have been extended.
This important conclusion is derived by comparing
simple counts of nebulae with measured luminosities,
corrected by energy-factors which must be applied to
such measures regardless of cosmological theory. The
uniform distribution is a plausible and welcome result.
Homogeneity within our sample seems so plausible, in
fact, that it has often been adopted as a preliminary
assumption. The apparent distribution indicated by
the crude observations is then described as a true,
uniform distribution plus apparent departures from
uniformity. The apparent departures can be expressed
as corrections to the measured luminosities of nebulae
at the limits of the various surveys, and these corrections, in turn,
can be compared with the red-shifts at
the same limits. The result, expressed in terms of
magnitude increments
 m, is
m, is
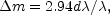 |
which agrees very closely with the energy-corrections
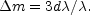 |
The energy-corrections, it will be recalled, are the total effects of red-shifts on apparent luminosities, provided red-shifts are not velocity-shifts. The latter interpretation seems to follow directly from the preliminary assumption of uniformity.
The assumption of uniformity has much to be said in its favour. If the distribution were not uniform, it would either increase with distance, or decrease. But we would not expect to find a distribution in which the density increases with distance, symmetrically in all directions. Such a condition would imply that we occupy a unique position in the universe, analogous, in a sense, to the ancient conception of a central earth. The hypothesis cannot be disproved but it is unwelcome and would be accepted only as a last resort in order to save the phenomena. Therefore, we disregard this possibility and consider the alternative, namely, a distribution which thins out with distance.
A thinning out would be readily explained in either of two ways. The first is space absorption. If the nebulae were seen through a tenuous haze, they would fade away faster than could be accounted for by distance and red-shifts alone, and the distribution, even if it were uniform, would appear to thin out. The second explanation is a super-system of nebulae, isolated in a larger world, with our own nebula somewhere near the centre. In this case the real distribution would thin out after all the proper corrections had been applied.
Both explanations seem plausible, but neither is permitted by the observations. The apparent departures from uniformity in the World Picture are fully compensated by the minimum possible corrections for redshifts on any interpretation. No margin is left for a thinning out. The true distribution must either be uniform or increase outward, leaving the observer in a unique position. But the unwelcome supposition of a favoured location must be avoided at all costs. Therefore, we accept the uniform distribution, and assume that space is sensibly transparent. Then the data from the surveys are simply and fully accounted for by the energy corrections alone - without the additional postulate of an expanding universe.
In this case all the empirical information we have concerning the observable region as a whole is internally consistent. The region appears to be thoroughly homogeneous - an insignificant sample of a universe which extends indefinitely. The conclusion would probably be accepted without hesitation if it were not for the fact that, at the moment, we do not know of any permissible interpretation of red-shifts other than actual motion, actual recession of the nebulae.
3 The linear law of red-shifts (omitting
recession factors) is
d /
/
 = kr, and may
be written
= kr, and may
be written
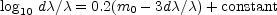 |
where d /
/
 is the mean red-shift
for nebulae of apparent magnitude m0;
m0 is the measured magnitude corrected for local
obscuration; the constant, which involves k and the intrinsic
luminosity of nebulae
(candle-power), is -4.707. From this equation red-shifts and the
corresponding energy-effects
is the mean red-shift
for nebulae of apparent magnitude m0;
m0 is the measured magnitude corrected for local
obscuration; the constant, which involves k and the intrinsic
luminosity of nebulae
(candle-power), is -4.707. From this equation red-shifts and the
corresponding energy-effects
 m =
3d
m =
3d /
/
 are
readily derived for the limiting magnitude of each survey.
Back.
are
readily derived for the limiting magnitude of each survey.
Back.