Comparison of Observations with Theory

Now let us return to the surveys, and reduce them all to the epoch, now, in accordance with the principles of relativistic cosmology. We wish to know the relative numbers of nebulae which an observer, in an expanding universe, would count to successive limits of apparent faintness. The problem is intricate but it has been thoroughly investigated, and the necessary formula is available in quite simple terms. ⁴ Actually, the expression is just that previously derived for uniform distribution in a stationary universe, plus two extra terms. One of the terms represents the recession factor, the other represents effects of spatial curvature.

If the use of a logarithm is permitted, the situation may be clearly represented by a pair of equations. If nebulae are uniformly distributed through a non-expanding universe in which red-shifts are not primarily velocity-shifts, then the numbers should be proportional to the volumes, and the surveys should conform (and actually do conform) with the relation

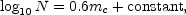where m_c is the limiting faintness expressed as a magnitude, corrected for local obscuration and for the energy-effects required by the mere presence of redshifts. ⁵ The corresponding relation for a homogeneous, expanding universe, obeying the relativistic laws of gravitation, is

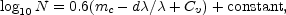where d / is the recession factor and C_v is the effect of spatial curvature. We wish to know whether or not the surveys can be fitted into the latter expression.

If both of the extra terms (for recession and for curvature) were absent, the surveys would clearly fit the formula because the situation would be precisely that in a stationary universe. Now suppose we introduce only one of the extra terms, namely, the recession factor. In this way we pass from a stationary universe to an expanding universe with negligible curvature, but we destroy the agreement with the observations. The distribution is no longer uniform. The recession factors introduce departures from uniformity in the law of distribution, just as they introduced departures from linearity in the law of red-shifts.

Fig. 3. The Law of Nebular Distribution on Alternative Interpretations of Red-Shifts. Each point represents an entire survey and indicates the average number of nebulae per square degree, N, brighter than the limiting magnitude of the survey, m. The black disks represent the observed magnitudes corrected for local obscuration and energy-effects only. They define the straight line, log10 N = 0.6m - 9.05, and indicate uniform distribution of nebulae in space when red-shifts are interpreted as not velocity-shifts. The open circles represent the magnitudes further corrected by recession factors, and determine a distribution (the dash line) which departs systematically from uniformity. Homogeneity may be restored by postulating sufficient spatial curvature to offset the displacements introduced by the recession factors.

⁴ The requisite formulae have been derived by various investigators. Those used in the present discussion were developed by R. C. Tolman (Relativity, Thermodynamics, and Cosmology, Clarendon Press, (1934) and adapted to the specific problem of the surveys by Hubble and Tolman (Mt. Wilson Contr., No. 527; Astrophysical Journal, 82, 302, 1935) Back.

⁵ The derivation is as follows. For uniform distribution numbers of nebulae N are proportional to volumes of space, and, consequently, to the cubes of the limiting distances r to which the counts are carried. Hence log₁₀ N = 3 log₁₀ r + constant. Among objects of the same candle-power the distances are proportional to the inverse square of the apparent luminosity l. Hence log₁₀ r = constant - 0.5 log₁₀ l. Apparent magnitudes m measure apparent luminosities on a logarithmic scale. By definition, m = constant - 2.5 log₁₀ l. Hence

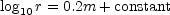and
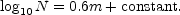