12.5.2. Effect of Energy Losses

Even if relativistic electrons are initially produced with a power law distribution, differential energy losses can alter the energy spectrum. Relativistic electrons lose energy by synchrotron radiation and by the inverse Compton effect, which are both proportional to the square of the energy; by ordinary bremsstrahlung and adiabatic expansion, which are directly proportional to the energy; and by ionization; which is approximately proportional to the logarithm of the energy. Approximating the logarithmic term by a constant, the rate of energy loss may be written

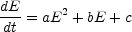(12.10)

If electrons are being supplied to the source at a rate N(E, t), then the equation of continuity describing the time dependence of the energy distribution N(E, t) is

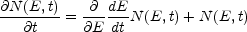(12.11)

If at t = 0

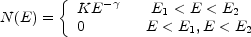(12.12)

and if synchrotron and inverse Compton losses dominate and there is no injection of new particles [N(E, t) = 0], then

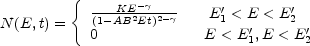(12.13)

where

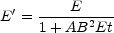Thus, even with an initial energy distribution extending to unlimited energy, there will be a cut-off at

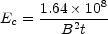(12.14)

and a corresponding cut-off in the synchrotron radiation spectrum. In the special case where ~ - 2, N(E, t) can become very large for energies slightly less than E_c because of the piling up near E_c of electrons with large initial energies as the result of their more rapid rate of energy loss. In this case, if E₂ is sufficiently large so that (E₂^' / E_c) ~ 1, then the radiation spectrum will become flat just below the upper cut-off frequency, _c = cBE_c². Above _c the spectrum sharply decreases rapidly for all values of .

If the distribution of electron pitch angles is random, then the cut-off frequency for each pitch angle differs. At low frequencies where energy losses are not important, the spectral index, , remains equal to its initial value ₀ = (1 - ) / 2. But at higher frequencies if the pitch angle of each electron remains constant (Kardashev, 1962), = (4/3 ₀ - 1). If on the other hand the pitch angle distribution is continuously made random, e.g., by irregularities in the magnetic field, then all the electrons see the same effective magnetic field and the spectrum shows the same sharp cut-off observed with a single pitch angle. The frequency at which synchrotron radiation loss is important is given by

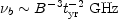(12.15)

If the relativistic electrons are continuously injected with Q(E) = KE^-₀, then for < _b the spectral index remains constant with = ₀. But at higher frequencies where the rate of energy loss is balanced by the injection of new particles, the equilibrium solution of Equation (12.11) with (N / t) = 0 gives = (₀ - 1/2).