13.3.3. Polarization

As described in Section 13.1, in a uniform magnetic field with a power law distribution of electron energies having an index p, the linear polarization, P_t(p), of a transparent source is perpendicular to the direction of the magnetic field and is given by

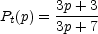(13.22)

which is of the order of 70% for typical values of p.

In the opaque portion of the spectrum, the polarization is parallel to the magnetic field and is given by

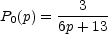(13.23)

so that P₀ is typically only about 10% or less. Observations of integrated polarization are typically much less than that predicted for a uniform field by at least an order of magnitude, presumably due to the random orientation of the magnetic fields.

The observed polarization position angle is modified by Faraday rotation (Section 1.2.2). Although most of the rotation occurs primarily within our galaxy (Section 1.5.4), some is internal to the sources. In a few cases, the internal rotation measure is surprisingly large with measured values up to several thousand radians per meter².

There appears to be no evidence for internal Faraday rotation in the compact radio sources. This places strict limits on the number of thermal electrons that can coexist with the relativistic electron cloud (Wardle 1977, Jones and O'Dell 1977). Indeed, the absence of Faraday rotation requires that the number of relativistic electrons must greatly exceed the number of cold (thermal) electrons, or that there are both electrons and positrons. Moreover, the number of low-energy relativistic electrons must be much less than the number expected from a power law extrapolation of the high-energy population. This has important implications for possible acceleration mechanisms, and would appear to exclude most stochastic processes.

The synchrotron radiation from a single electron is elliptically polarized and has a large circular component which is mostly canceled if the pitch angle distribution is isotropic. However, there is still a small net circular polarization, since there are more electrons in the solid angle defined by + d than in the one defined by - d. This effect is particularly important if the cone of radiation of a single electron ( ~ mc² / E) is large, which will occur at very low frequencies or in regions of high magnetic field strength (small values of electron energy).

In a uniform magnetic field of B gauss, and isotropic distribution of electron pitch angles, the integrated circular polarization is P_c ~ (3B / )^1/2 at a frequency (Sciama and Rees 1967). In a few sources the degree of circular polarization has been measured to be ~ 0.01% to 0.1% near 1 GHz. This corresponds to magnetic fields of ~ 3 × 10^-5±1 gauss - in good apparent agreement with the values derived from the synchrotron self-absorption cutoff frequency and the angular size.