13.4.2. Jet Physics

Since we have no direct way of estimating the density and velocity of a radio-emitting jet, a maze of indirect arguments and physical assumptions is made to deduce the nature of the phenomena. However, within the framework of a set of physical assumptions, many deductions can be made, and if we do not make a completely incorrect assumption, (for example, that the radio brightness is due to the incoherent synchrotron process), we can sometimes limit the physical conditions to a fairly narrow range of possibilities. Basically, we have the radio brightness and its linear polarization at one or more frequencies to work with. We also may have some knowledge of the external conditions from X-ray or optical observations.

(a) Straight Jets

Let us assume that a jet is a collimated flow consisting of thermal and relativistic gas initially moving with some velocity v and some radius r. The brightness is then affected by (1) radiation losses, (2) adiabatic gains or losses, and (3) other energy gains or losses by the relativistic electrons. As a jet expands, the particles in the jet will gain or lose energy, consistent with their equation of state. In particular, the relativistic particle energy density, , in a volume V will change as V^-4/3, or the the total energy of a single particle will vary as E V^-1/3.

Thus, in the cylindrical geometry of a jet, as the radius of the jet, r_j, increases, each relativistic electron should lose energy to the expansion as E r_j^-2/9.

If magnetic flux is conserved then B_|| r_j^-1, and B r_j^-2.

If the velocity of the jet, v_j, remains constant and no energy is added to the particles or magnetic field from other sources, the luminosity of all observed jets would decrease much faster than is observed (e.g., Bridle and Perley 1984). Thus one of these assumptions must be incorrect. If the velocity decreases, then the density of particles and the perpendicular magnetic field strength will increase, thus counteracting the effects of any expansion. Combining both effects for a power law energy spectrum, the intensity, I varies as

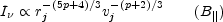or

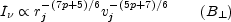Thus, the jet can actually brighten with certain combinations of parameters. However, if v_j decreases sufficiently, then radiation losses can become important. Also, particles lose energy through inverse Compton scattering to the 3 K background, so the net rate at which particles lose energy reaches a minimum at a magnetic field strength of a few microgauss. Thus, it is not possible to explain the brightness of jets by simply letting v decrease indefinitely. If adiabatic effects alone cannot explain the brightness distribution, then some nonadiabatic effect must be contributing to the energy in the particles and/or fields. The most obvious source is probably the energy in the bulk flow of any thermal plasma in the jet. This could be transferred to the particles through interactions with shocks or through plasma waves in a turbulent plasma. These processes, however, seem to work best when adding energy to already relativistic particles. Theoretical calculations and in situ space observations show they are very inefficient in accelerating thermal particles, especially electrons, to relativistic energies (Lee 1983). Since these and other processes are uncertain in their details, usually it is simply assumed that a fraction, , of the kinetic energy in the jet is converted to relativistic electron energy. Thus,

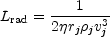(13.31)

where L_rad is the total emitted radiation and _j is the density of thermal particles in the jet.

Equation (13.31) is called the kinetic luminosity equation. Rough estimates for jet or total-source requirements are often made by simply using the total luminosity of (half) of the source as L_rad and estimating from the observed Faraday depolarization or the density of the background gas. Clearly, a better approach would be to combine at least adiabatic effects with particle acceleration but this has rarely been done.

(b) Bent Jets

If as in the wide-angle tails or narrow-angle tails, the jet is bent, an additional constraint exists, since the time-independent Euler's equation should apply or

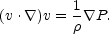(13.32)

If R is the scale length over the jet bends, then (v ^. )v v_b² / R. Then

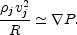(13.33)

A galaxy moving with velocity v_g through an intracluster medium with density _icm experiences a ram pressure _icm v_g². This pressure is exerted over a scale length h. If the jet is directly exposed to the intracluster medium, then h = r_j. On the other hand, the jet maybe inside the interstellar medium of a galaxy. Then h is the pressure scale height in the galaxy. In any case, one can write

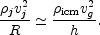(13.34)

Combining the kinetic luminosity equation (13.31) with the Euler's equation in the form (13.32), we can eliminate one of the common variables. For example, eliminating v_b we can get

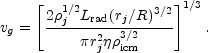(13.35)

For cases involving narrow-angle tails moving at 10³ km s^-1 with respect to the external medium, one can find acceptable applications of this equation. However, for the wide-angle tails, one has a higher luminosity to explain and strong evidence in some cases that the parent galaxy is moving very slowly or not at all with respect to the intracluster medium. Thus, a simple picture of motion causing the bending of wide-angle tails appears to fail. More complete models including adiabatic effects or other energy sources for the particles such as turbulence in the gas entrained from the intracluster medium appear to be necessary.