C. Inflation and dark energy

The negative active gravitational mass density associated with a positive cosmological constant is an early precursor of the inflation picture of the early universe; inflation in turn is one precursor of the idea that might generalize into evolving dark energy.

To begin, we review some aspects of causal relations between events in spacetime. Neglecting space curvature, a light ray moves proper distance dl = a(t) dx = dt in time interval dt, so the integrated coordinate displacement is

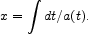(26)

If ₀ = 0 this integral converges in the past -- we see distant galaxies that at the time of observation cannot have seen us since the singular start of expansion at a = 0. This "particle horizon problem" is curious: how could distant galaxies in different directions in the sky know to look so similar? The inflation idea is that in the early universe the expansion history approximates that of de Sitter's (1917) solution to Einstein's field equation for > 0 and T_µ = 0 in Eq. (20). We can choose the coordinate labels in this de Sitter spacetime so space curvature vanishes. Then Eqs. (11) and (12) say the expansion parameter is

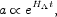(27)

where H is a constant. As one sees by working the integral in Eq. (26), here everyone can have seen everyone else in the past. The details need not concern us; for the following discussion two concepts are important. First, the early universe acts like an approximation to de Sitter's solution because it is dominated by a large effective cosmological "constant", or dark energy density. Second, the dark energy is modeled as that of a near homogeneous field, .

In this scalar field model, motivated by grand unified models of very high energy particle physics, the action of the real scalar field, (in units chosen so Planck's constant is unity) is

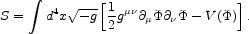(28)

The potential energy density V is a function of the field , and g is the determinant of the metric tensor. When the field is spatially homogeneous (in the line element of Eq. [15]), and space curvature may be neglected, the field equation is

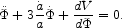(29)

The stress-energy tensor of this homogeneous field is diagonal (in the rest frame of an observer moving so the universe is seen to be isotropic), with time and space parts along the diagonal

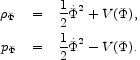(30)

If the scalar field varies slowly in time, so that 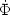² << V, the field energy approximates the effect of Einstein's cosmological constant, with p - .

The inflation picture assumes the near exponential expansion of Eq. (27) in the early universe lasts long enough that every bit of the present observable universe has seen every other bit, and presumably has discovered how to relax to almost exact homogeneity. The field may then start varying rapidly enough to produce the entropy of our universe, and the field or the entropy may produce the baryons, leaving small or zero. But one can imagine the late time evolution of is slow. If slower than the evolution in the mass density in matter, there comes a time when again dominates, and the universe appears to have a cosmological constant.

A model for this late time evolution assumes a potential of the form

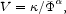(31)

where the constant has dimensions of mass raised to the power + 4. For simplicity let us suppose the universe after inflation but at high redshift is dominated by matter or radiation, with mass density , that drives power law expansion, a tⁿ. Then the power law solution to the field equation (29) with the potential in Eq. (31) is

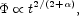(32)

and the ratio of the mass densities in the scalar field and in matter or radiation is

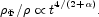(33)

In the limit where the parameter approaches zero, is constant, and this model is equivalent to Einstein's .

When > 0 the field in this model grows arbitrarily large at large time, so 0, and the universe approaches the Minkowskian spacetime of special relativity. This is within a simple model, of course. It is easy to imagine that in other models approaches a constant positive value at large time, and spacetime approaches the de Sitter solution, or passes through zero and becomes negative, causing spacetime to collapse to a Big Crunch.

The power law model with > 0 has two properties that seem desirable. First, the solution in Eq. (32) is said to be an attractor (Ratra and Peebles, 1988) or tracker (Steinhardt, Wang, and Zlatev, 1999), meaning it is the asymptotic solution for a broad range of initial conditions at high redshift. That includes relaxation to a near homogeneous energy distribution even when gravity has collected the other matter into nonrelativistic clumps. Second, the energy density in the attractor solution decreases less rapidly than that of matter and radiation. This allows us to realize the scenario: after inflation but at high redshift the field energy density is small so it does not disturb the standard model for the origin of the light elements, but eventually dominates and the universe acts as if it had a cosmological constant, but one that varies slowly with position and time. We comment on details of this model in Sec III.E.