Annu. Rev. Astron. Astrophys. 2002. 40: 643-680 Copyright © 2002 by Annual Reviews. All rights reserved

2. THE SUNYAEV-ZEL'DOVICH EFFECT

2.1. Thermal Sunyaev-Zel'dovich Effect

The Sunyaev-Zel'dovich effect (SZE) is a small spectral distortion of the cosmic microwave background (CMB) spectrum caused by the scattering of the CMB photons off a distribution of high energy electrons. Here we focus only on the SZE caused by the hot thermal distribution of electrons provided by the intra-cluster medium (ICM) of galaxy clusters. CMB photons passing through the center of a massive cluster have only a 1% probability of interacting with an energetic ICM electron. The resulting inverse Compton scattering preferentially boosts the energy of the CMB photon by roughly k_B T_e / m_e c² causing a small ( 1 mK) distortion in the CMB spectrum. Figure 1 shows the SZE spectral distortion for a fictional cluster that is over 1000 times more massive than a typical cluster to illustrate the small effect. The SZE appears as a decrease in the intensity of the CMB at frequencies 218 GHz and as an increase at higher frequencies.

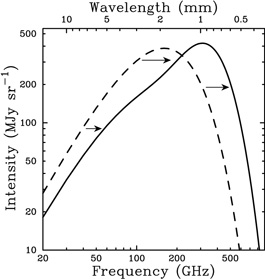Figure 1. The Cosmic Microwave Background (CMB) spectrum, undistorted (dashed line) and distorted by the Sunyaev-Zel'dovich effect (SZE) (solid line). Following Sunyaev & Zel'dovich (1980a) to illustrate the effect, the SZE distortion shown is for a fictional cluster 1000 times more massive than a typical massive galaxy cluster. The SZE causes a decrease in the CMB intensity at frequencies 218 GHz and an increase at higher frequencies.

The derivation of the SZE can be found in the original papers of Sunyaev and Zel'dovich (Sunyaev & Zel'dovich, 1970, 1972), in several reviews (Sunyaev & Zel'dovich, 1980a, Rephaeli, 1995, Birkinshaw, 1999), and in a number of more recent contributions which include relativistic corrections (see below for references). This review discusses the basic features of the SZE that make it a useful cosmological tool.

The SZE spectral distortion of the CMB expressed as a temperature change T_SZE at dimensionless frequency x (h ) / (k_B T_CMB) is given by

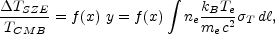(1)

where y is the Compton y-parameter, which for an isothermal cluster equals the optical depth, _e, times the fractional energy gain per scattering, _T is the Thomson cross-section, n_e is the electron number density, T_e is the electron temperature, k_B is the Boltzmann constant, m_e c² is the electron rest mass energy, and the integration is along the line of sight. The frequency dependence of the SZE is

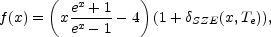(2)

where _SZE(x, T_e) is the relativistic correction to the frequency dependence. Note that f (x) - 2 in the non-relativistic and Rayleigh-Jeans (RJ) limits.

It is worth noting that T_SZE / T_CMB is independent of redshift as shown in Eq. 1. This unique feature of the SZE makes it a potentially powerful tool for investigating the high redshift universe.

Expressed in units of specific intensity, common in millimeter SZE observations, the thermal SZE is

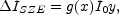(3)

where I₀ = 2(k_B T_CMB)³ / (hc)² and the frequency dependence is given by

(4)

T_SZE and I_SZE are simply related by the derivative of the blackbody with respect to temperature, |dB / dT|.

The spectral distortion of the CMB spectrum by the thermal SZE is shown in Figure 2 (solid line) for a realistic massive cluster (y = 10^-4) in units of intensity (left panel) and Rayleigh-Jeans (RJ) brightness temperature (right panel). The RJ brightness is shown because the sensitivity of a radio telescope is calibrated in these units. It is defined simply by I = (2k_B ² / c²) T_RJ where I is the intensity at frequency , k_B is Boltzmann's constant, and c is the speed of light. The CMB blackbody spectrum, B(T_CMB), multiplied by 0.0005 (dotted line) is also shown for comparison. Note that the spectral signature of the thermal effect is distinguished readily from a simple temperature fluctuation of the CMB. The kinetic SZE distortion is shown by the dashed curve (Section 2.2). In the non-relativistic regime, it is indistinguishable from a CMB temperature fluctuation.

Figure 2. Spectral distortion of the cosmic microwave background (CMB) radiation due to the Sunyaev-Zel'dovich effect (SZE). The left panel shows the intensity and the right panel shows the Rayleigh Jeans brightness temperature. The thick solid line is the thermal SZE and the dashed line is the kinetic SZE. For reference the 2.7 K thermal spectrum for the CMB intensity scaled by 0.0005 is shown by the dotted line in the left panel. The cluster properties used to calculate the spectra are an electron temperature of 10 keV, a Compton y parameter of 10-4, and a peculiar velocity of 500 km s-1.

The gas temperatures measured in massive galaxy clusters are around k_B T_e ~ 10 keV (Mushotzky & Scharf, 1997, Allen & Fabian, 1998) and are measured to be as high as ~ 17 keV in the galaxy cluster 1E 0657 - 56 (Tucker et al, 1998). The mass is expected to scale with temperature roughly as T_e M^2/3. At these temperatures, electron velocities are becoming relativistic and small corrections are required for accurate interpretation of the SZE. There has been considerable theoretical work to include relativistic corrections to the SZE (Wright, 1979, Fabbri, 1981, Rephaeli, 1995, Rephaeli & Yankovitch, 1997, Stebbins, 1997, Itoh et al, 1998, Challinor & Lasenby, 1998, Sazonov & Sunyaev, 1998a, Sazonov & Sunyaev, 1998b, Nozawa et al, 1998b, Challinor & Lasenby, 1999, Molnar & Birkinshaw, 1999, Dolgov et al, 2001). All of these derivations agree for k_B T_e 15 keV, appropriate for galaxy clusters. For a massive cluster with k_B T_e ~ 10 keV (k_B T_e / m_e c² ~ 0.02) the relativistic corrections to the SZE are of order a few percent in the RJ portion of the spectrum, but can be substantial near the null of the thermal effect. Convenient analytical approximations to fifth order in k_B T_e / m_e c² are presented in Itoh et al (1998).

Particularly relevant for finding clusters with an SZE survey is the integrated SZE signal. Because the SZE signal is the integrated pressure, integrating over the solid angle of the cluster provides a sum of all of the electrons in the cluster weighted by temperature. This provides a relatively clean measure of the total thermal energy of the cluster. Integrating the SZE over the solid angle of the cluster, d = dA / D_A², gives

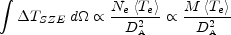(5)

where N_e is the total number of electrons in the clusters, <T_e> is the mean electron temperature, D_A is the angular diameter distance, and M is the mass of the cluster (either gas or total mass as M_gas = M_total f_g, where f_g is the gas mass fraction). The integrated SZE flux is simply the temperature weighted mass of the cluster divided by D_A². The angular diameter distance D_A(z) is fairly flat at high redshift. Also, a cluster of a given mass will be denser and therefore hotter at high redshift because the universal matter density increases as (1 + z)³. Therefore, one expects an SZE survey to detect all clusters above some mass threshold with little dependence on redshift (see Section 4.2).

The most important features of the thermal SZE are: 1) it is a small spectral distortion of the CMB of order ~ 1 mK, which is proportional to the cluster pressure integrated along the line of sight [Eq. 1]; 2) it is independent of redshift; 3) it has a unique spectral signature with a decrease in the CMB intensity at frequencies 218 GHz and an increase at higher frequencies; and 4) the integrated SZE flux is proportional to the temperature weighted mass of the cluster (total thermal energy of the cluster) implying that SZE surveys will have a mass threshold nearly independent of redshift.

2.2. Kinetic Sunyaev-Zel'dovich Effect

If the cluster is moving with respect to the CMB rest frame there will be an additional spectral distortion due to the Doppler effect of the cluster bulk velocity on the scattered CMB photons. If a component of the cluster velocity, v_pec, is projected along the line of sight to the cluster, then the Doppler effect will lead to an observed distortion of the CMB spectrum referred to as the kinetic SZE. In the non-relativistic limit, the spectral signature of the kinetic SZE is a pure thermal distortion of magnitude

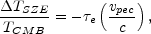(6)

where v_pec is along the line of sight; i.e., the emergent spectrum is still described completely by a Planck spectrum, but at a slightly different temperature, lower (higher) for positive (negative) peculiar velocities (Sunyaev & Zel'dovich, 1972, Phillips, 1995, Birkinshaw, 1999, see Figure 2).

Relativistic perturbations to the kinetic SZE are due to the Lorentz boost to the electrons provided by the bulk velocity (Nozawa et al, 1998a, Sazonov & Sunyaev, 1998a). The leading term is of order (k_B T_e / m_e c²)(v_pec / c) and for a 10 keV cluster moving at 1000 km s^-1 the effect is about an 8% correction to the non-relativistic term. The (k_B T_e / m_e c²)²(v_pec / c) term is only about 1% of the non-relativistic kinetic SZE and the (v_pec / c)² term is only 0.2%.

2.3. Polarization of the Sunyaev-Zel'dovich Effect

The scattering of the CMB photons by the hot ICM electrons can result in polarization at levels proportional to powers of (v_pec / c) and _e. The largest polarization is expected from the anisotropic optical depth to a given location in the cluster. For example, toward the outskirts of a cluster one expects to see a concentric (radial) pattern of the linear polarization at frequencies where the thermal SZE is positive (negative). Plots of the polarization pattern are presented in Sazonov & Sunyaev (1999). Nonspherical morphology for the electron distributions will lead to considerably complicated polarization patterns. The peak polarization of this signal will be order _e times the SZE signal, i.e., of order 0.025(k_B T_e / m_e c²) _e² times the CMB intensity. For a massive cluster with _e = 0.01, the effect would be at the 0.1 µK level toward the edge of the cluster. In principle, this effect could be used to measure the optical depth of the cluster and therefore separate T_e and _e from a measurement of the thermal SZE (see Eq. 1).

It can be shown that polarization of the SZE comes entirely from the quadrupole component of the local radiation field experienced by the scattering electron. In the case above, the quadrupole component at the outskirts of the cluster is due to the anisotropy in the radiation field in the direction of the cluster center due to the SZE. Sunyaev and Zel'dovich discussed polarization due to the motion of the cluster with respect to the CMB and transverse to our line of sight (Sunyaev & Zel'dovich, 1980b, see also Sazonov & Sunyaev, 1999). In this case, the quadrupole comes from the Doppler shift. They found the largest terms to be of order 0.1_e(v_pec / c)² and 0.025_e²(v_pec / c) of the CMB intensity. The latter term, second order in _e, can be thought of as imperfect cancellation of the dipole term due to the anisotropic optical depth. Using _e = 0.01 and a bulk motion of 500 km s^-1, results in polarization levels of order 10 nK, far beyond the sensitivity of current instrumentation.

The CMB as seen by the cluster electrons will have a quadrupole component and therefore the electron scattering will lead to linear polarization. This mechanism could possibly be used to trace the evolution of the CMB quadrupole if polarization measurements could be obtained for a large number of clusters binned in direction and redshift (Kamionkowski & Loeb, 1997, Sazonov & Sunyaev, 1999). Sazonov and Sunyaev calculated the expected polarization level and found the maximum CMB quadrupole induced polarization is 50(_e/0.01) nK, somewhat higher than the expected velocity induced terms discussed above. The effect is again too small to expect detection in the near future. However, by averaging over many clusters, detecting this polarization might be possible with future satellite missions.