Our present understanding of the beginning of the universe is based upon the remarkably successful theory of the Hot Big Bang. We believe that our universe began about 15 billion years ago as a hot, dense, nearly uniform sea of radiation a minute fraction of its present size (formally an infinitesimal singularity). If inflation occurred in the first fraction of a second, the universe became matter dominated while expanding exponentially and then returned to radiation domination by the reheating caused by the decay of the inflaton. Baryonic matter formed within the first second, and the nucleosynthesis of the lightest elements took only a few minutes as the universe expanded and cooled. The baryons were in the form of plasma until about 300,000 years after the Big Bang, when the universe had cooled to a temperature near 3000 K, sufficiently cool for protons to capture free electrons and form atomic hydrogen; this process is referred to as recombination. The recombination epoch occurred at a redshift of 1100, meaning that the universe has grown over a thousand times larger since then. The ionization energy of a hydrogen atom is 13.6 eV, but recombination did not occur until the universe had cooled to a characteristic temperature (kT) of 0.3 eV (Padmanabhan, 1993). This delay had several causes. The high entropy of the universe made the rate of electron capture only marginally faster than the rate of photodissociation. Moreover, each electron captured directly into the ground state emits a photon capable of ionizing another newly formed atom, so it was through recombination into excited states and the cooling of the universe to temperatures below the ionization energy of hydrogen that neutral matter finally condensed out of the plasma. Until recombination, the universe was opaque to electromagnetic radiation due to scattering of the photons by free electrons. As recombination occurred, the density of free electrons diminished greatly, leading to the decoupling of matter and radiation as the universe became transparent to light.
The Cosmic Background Radiation (CBR) released during this era of decoupling has a mean free path long enough to travel almost unperturbed until the present day, where we observe it peaked in the microwave region of the spectrum as the Cosmic Microwave Background (CMB). We see this radiation today coming from the surface of last scattering (which is really a spherical shell of finite thickness) at a distance of nearly 15 billion light years. This Cosmic Background Radiation was predicted by the Hot Big Bang theory and discovered at an antenna temperature of 3K in 1964 by Penzias & Wilson (1965). The number density of photons in the universe at a redshift z is given by (Peebles, 1993)
 |
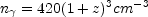(1) |
where (1 + z) is the factor by which the linear scale of the universe has expanded since then. The radiation temperature of the universe is given by T = T0(1 + z) so it is easy to see how the conditions in the early universe at high redshifts were hot and dense.
The CBR is our best probe into the conditions of the early
universe. Theories of the formation of large-scale structure
predict the existence of slight inhomogeneities in the distribution of
matter in the early universe which underwent gravitational
collapse to form galaxies, galaxy clusters, and superclusters. These
density inhomogeneities lead to temperature anisotropies in the CBR
due to a combination of intrinsic temperature fluctuations and
gravitational blue/redshifting of the photons leaving under/overdense
regions. The DMR (Differential Microwave Radiometer)
instrument of the Cosmic Background Explorer (COBE) satellite
discovered primordial temperature
fluctuations on angular scales larger than 7° of order
T / T
= 10-5
(Smoot et al.,
1992).
Subsequent observations of the CMB have
revealed temperature anisotropies on smaller
angular scales which correspond to the physical scale of
observed structures such as galaxies and clusters of galaxies.
There were three main processes by which this radiation interacted with
matter in the first few hundred thousand years: Compton scattering,
double Compton scattering, and thermal bremsstrahlung.
The simplest interaction of matter and radiation is Compton
scattering of a single photon off a free electron,
+
e- 
+
e-. The photon will transfer
momentum and energy to the electron if it has significant energy in the
electron's rest frame. However, the scattering will be
well approximated by Thomson scattering if the photon's energy in
the rest frame of the electron is significantly less than the rest mass,
h
<<
me c2.
When the electron is relativistic, the photon is blueshifted by
roughly a factor
in
energy when viewed from the
electron rest frame, is then emitted at almost the same energy in the
electron rest frame, and is blueshifted by another factor of
when retransformed to the observer's frame. Thus, energetic
electrons can efficiently transfer energy
to the photon background of the universe.
This process is referred to as Inverse Compton scattering.
The combination of cases where the photon gives energy to the electron
and vice versa allows Compton scattering to generate thermal equilibrium
(which is impossible in the Thomson limit of elastic scattering).
Compton scattering conserves the number of photons.
There exists a similar process, double Compton scattering,
which produces (or absorbs) photons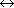, e- +
e- +
+
.
Another electromagnetic interaction which occurs in the plasma of the early
universe is Coulomb scattering. Coulomb scattering establishes
and maintains thermal equilibrium among the baryons of the photon-baryon
fluid without affecting the
photons. However, when electrons encounter ions they experience an
acceleration and therefore emit electromagnetic radiation. This is called
thermal bremsstrahlung or free-free emission. For an ion X,
we have e- + X
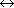e- + X +
. The
interaction can occur in reverse because of the ability of the charged
particles to absorb incoming photons; this is called free-free
absorption. Each charged
particle emits radiation, but the acceleration is proportional to the mass,
so we can usually view the electron as being accelerated in the fixed
Coulomb field of the much heavier ion.
Bremsstrahlung is dominated by electric-dipole radiation
(Shu, 1991)
and can also produce and absorb photons.
The net effect is that Compton scattering is dominant for temperatures above 90 eV whereas bremsstrahlung is the primary process between 90 eV and 1 eV. At temperatures above 1 keV, double Compton is more efficient than bremsstrahlung. All three processes occur faster than the expansion of the universe and therefore have an impact until decoupling. A static solution for Compton scattering is the Bose-Einstein distribution,
 |
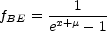(2) |
where µ is a dimensionless chemical potential (Hu, 1995). At high optical depths, Compton scattering can exchange enough energy to bring the photons to this Bose-Einstein equilibrium distribution. A Planckian spectrum corresponds to zero chemical potential, which will occur only when the number of photons and total energy are in the same proportion as they would be for a blackbody. Thus, unless the photon number starts out exactly right in comparison to the total energy in radiation in the universe, Compton scattering will only produce a Bose-Einstein distribution and not a blackbody spectrum. It is important to note, however, that Compton scattering will preserve a Planck distribution,
 |
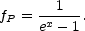(3) |
All three interactions will preserve a thermal spectrum if one is achieved at any point. It has long been known that the expansion of the universe serves to decrease the temperature of a blackbody spectrum,
 |
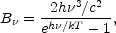(4) |
but keeps it thermal
(Tolman, 1934).
This occurs because both the frequency and temperature decrease as (1 +
z) leaving
h / kT
unchanged during expansion. Although
Compton scattering alone cannot produce a Planck distribution, such a
distribution will remain unaffected by electromagnetic interactions or the
universal expansion once it is achieved. A non-zero
chemical potential will be reduced to zero by double Compton scattering
and, later, bremsstrahlung which will create and absorb photons until the
number density matches the energy and a thermal distribution of zero
chemical potential is achieved. This results in the thermalization
of the CBR at redshifts much greater than that of recombination.
Thermalization, of course, should only be able to create an equilibrium temperature over regions that are in causal contact. The causal horizon at the time of last scattering was relatively small, corresponding to a scale today of about 200 Mpc, or a region of angular extent of one degree on the sky. However, observations of the CMB show that it has an isotropic temperature on the sky to the level of one part in one hundred thousand! This is the origin of the Horizon Problem, which is that there is no physical mechanism expected in the early universe which can produce thermodynamic equilibrium on superhorizon scales. The inflationary universe paradigm (Linde, 1982; Guth, 1981; Albrecht & Steinhardt, 1982) solves the Horizon Problem by postulating that the universe underwent a brief phase of exponential expansion during the first second after the Big Bang, during which our entire visible Universe expanded out of a region small enough to have already achieved thermal equilibrium.