Annu. Rev. Astron. Astrophys. 2003. 41: 191-239 Copyright © 2003 by Annual Reviews. All rights reserved

4. HYDROSTATIC EQUILIBRIUM AND MASS DETERMINATIONS

Evidence for dark halos in elliptical galaxies from stellar velocities has been slow in coming because of uncertainties in geometrical projection and in the anisotropy of stellar orbits as well as the inherent faintness of starlight beyond R_e where dark matter may begin to dominate the potential. Nevertheless, recent optical studies have revealed the presence of outwardly increasing mass to light ratios consistent with a dark matter contribution that is appreciable but not dominant at ~ R_e (Saglia et al 1992; Carollo et al 1995; Rix et al 1997; Gerhard et al 1998; Emsellem et al. 1999; Matthias & Gerhard 1999). Gravitational lensing of background objects provides independent evidence for a dark matter component in elliptical galaxies and their surrounding groups (e.g. Keeton 2001). Fortunately, the X-ray emitting hot gas allows in principle a much better determination of the total mass profile to very large radii. Accurate mass determinations require high quality X-ray observations of the gas density and (especially) temperature profiles plus reasonable assurance that the gas is in hydrostatic equilibrium and that gas pressure dominates. The mass distribution can only be determined for rather massive E galaxies, L_B L_{B, crit}, in which the X-ray emission is dominated by gas, not stellar sources.

Hydrostatic equilibrium requires that systematic and turbulent hot gas velocities are subsonic. Information moving at the sound speed in the hot gas in E galaxies, ( P / )^1/2 ~ 513 T_keV^1/2 km s^-1, crosses the optical half-light radius R_e ~ 10 kpc in only t_sc ~ 2 × 10⁷ years. If the hot gas is losing energy by radiative losses, it should flow inward at a rate ~ L_{x, bol} / (5kT / 2 µm_p) 1.5 M yr^-1 where L_{x, bol} ~ 5 × 10⁴¹ erg s^-1 is a typical X-ray bolometric luminosity for massive E galaxies. Using n_e(R_e) ~ 0.01 cm^-3 for a typical hot gas density at R_e, the systematic inflow velocity, u ~ / n_e(R_e) m_p 4 R_e² ~ 5 km s^-1, is highly subsonic, consistent with hydrostatic equilibrium. Less is known about the magnitude of turbulent motions in the hot gas, but radial velocities of diffuse optical emission lines from gas at T ~ 10⁴ K in the central regions of E galaxies (e.g. Caon et al. 2000), v_turb 150 km s^-1, suggest subsonic motion, assuming this cold gas comoves with the local hot gas.

The condition for hydrostatic equilibrium dP_tot / dr = - GM / r² allows a direct determination of the total mass of stars and dark matter within each radius:

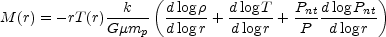(1)

where m_p is the proton mass and µ = 0.61 is the molecular weight for full ionization. In addition to the gas pressure P, an additional non-thermal turbulent, magnetic or cosmic ray pressure P_nt may be present. In ellipticals containing strong radio sources Faraday depolarization at radio frequencies provides direct evidence for P_nt (e.g. Garrington et al. 1988; Garrington & Conway 1991), but this pressure is usually ignored in most E galaxy mass determinations. Non-radiating relativistic protons may also be present (e.g. Fabian et al. 2002a), so it is unclear if P_nt can always be ignored.

The total integrated mass M(r) can be estimated by using the average temperature within some radius. Loewenstein & White (1999) studied the ratio of the dimensional coefficients in the equation above, = <>² / (k <T> / µ m_p) where <>² GM(r) / r is the central stellar velocity dispersion (assumed to be isotropic) and <T> is the mean hot gas temperature within 6R_e determined from fits to the thermal X-ray spectrum. Loewenstein & White considered an optically complete sample of over 40 E galaxies (Davis & White 1996). Using accurate stellar mass profiles normalized to the fundamental plane, they determined that 0.75 - 1.2 should be expected in the absence of dark matter. The observed values, 0.6 ± 0.1, clearly require a dark matter component. Both the gas and the dark matter are hotter than the central stars. Loewenstein & White conclude that dark matter increases from stellar values at the origin <_V> <M / L_V> 10h₇₀ M / L_V, to <_V> 22h₇₀ M / L_V, within 6R_e. Extended dark halos are a common property of all bright ellipticals.

For a few bright E galaxies both T(r) and n_e(r) can be determined and Equation (1) can be solved directly for the total mass profile M(r). Figure 2a shows the electron density profile in NGC 4472, a well-observed massive E1 galaxy and the brightest galaxy in the Virgo cluster, at an assumed distance of d = 17 Mpc (n_e d^-1/2). The hot gas density profiles may have small flattened cores but vary as n_e r^-p at larger radii with p 1 - 1.5, so the gas mass increases outward. Using Einstein HRI data Trinchieri, Fabbiano & Canizares (1986) showed that the optical and X-ray surface brightness profiles are almost identical for three bright Virgo ellipticals, NGC 4649, NGC 4636 and NGC 4472, so that n_e². This remarkable result is illustrated again in Figure 2a where n_{e *}^1/2 is seen to hold over a wide range in galactic radius.

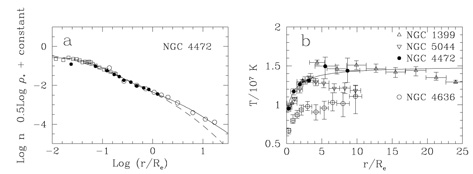Figure 2. (2a Left panel:) The observed and azimuthally averaged electron density profile n(r) in NGC 4472 is shown as a function of radius normalized to the effective radius Re = 8.57 kpc at distance d = 17 Mpc. The observations are from Einstein (Trinchieri, Fabbiano, & Canizares 1986) (filled circles) and ROSAT (Irwin & Sarazin 1996) (open circles); for the inner region we have Abel-inverted Chandra surface brightness data from Loewenstein et al. (2001) (open squares) and normalized them to previous observations. The solid line is an analytic fit to the observations. The dashed line is the square root of the stellar density *1/2(r) normalized to n at r = Re. (2b Right panel:) Typical temperature profiles for several bright E galaxies, taken from Brighenti & Mathews (1997a), based on the following sources: NGC 1399: ROSAT PSPC from Jones et al. (1997); NGC 5044: ROSAT PSPC from David et al. (1994); NGC 4636: ROSAT PSPC from Trinchieri et al. (1994); NGC 4472: ROSAT HRI AND PSPC from Irwin & Sarazin (1996). The solid line is an approximate analytic fit to T(r) for NGC 4472.

Figure 2b shows the hot gas temperature profiles for several massive E galaxies. The temperature in these group-dominant E galaxies rises from a minimum value near the galactic center to a maximum at several R_e and, if the gas is sufficiently extended, is either uniform or slowly decreasing beyond (Brighenti & Mathews 1997 and references therein), sometimes extending to 10R_e. (In cluster-centered E galaxies the temperature continues to rise to the cluster gas temperature.) The radiative cooling time at constant pressure in the hot gas in NGC 4472 is quite short, t_cool 10⁸r_kpc^1.2 yrs, but greater than the dynamical time t_dyn 3 × 10⁶ r_kpc^0.85 yrs. The entropy factor Tn^-2/3 for NGC 4472 is relatively flat within r ~ 0.55 kpc, suggesting local heating (David et al. 2001), then increases monotonically with radius, Tn^-2/3 6.5 × 10⁷r_kpc^0.8712 K cm², as required for convective stability. Recent Chandra observations often show surface brightness fluctuations and cavities, sometimes extending to ~ R_e, that suggest deviations from hydrostatic equilibrium.

The total mass M_tot(r) profile for NGC 4472 determined from Equation (1) (with P_nt = 0 and data from Figs. 2a and 2b) is plotted in Figure 3a. Also shown is the stellar mass distribution M_*(r) based on a de Vaucouleurs profile _*,deV(r) (total mass: M_*t = 7.26 × 10¹¹ M; effective radius: R_e = 1.733' = 8.57 kpc) with a core (r) = _*,deV(r_b)(r / r_b)^-0.90 within the break radius r_b = 2.41" = 200 pc (Gebhardt et al. 1996; Faber et al. 1997). It is remarkable that the total mass M_tot(r) in Figure 3a determined with Equation (1) agrees quite well with the de Vaucouleurs mass profile in the range 0.1 r / R_e 1. The best fitting stellar profile corresponds to a mass to light ratio of _B M / L_B 7, slightly less than _B = 9.2 determined for NGC 4472 from axisymmetric stellar models near the galactic core (van der Marel 1991). This consistency of X-ray and stellar mass profiles suggests that the stellar mass to light ratio in NGC 4472 does not change greatly with galactic radius in 0.1 r / R_e 1 (Brighenti & Mathews 1997a; also for NGC 720: Buote et al. 2002a). As X-ray observations improve we expect that they will provide much information on the stellar mass to light ratio for r R_e. At small radii r 0.03R_e in NGC 4472, M_tot is less than M_*. This may indicate some additional non-thermal pressure P_nt in this region or a deviation from hydrostatic equilibrium. Like most bright E galaxies, NGC 4472 contains a faint double lobe radio source that extends to ~ 0.5R_e (Ekers & Kotanyi 1978).

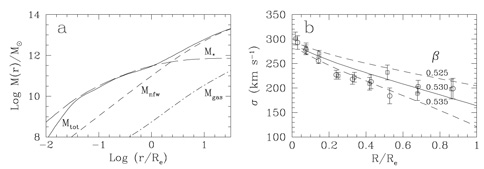Figure 3. (3a Left panel:) The total mass Mtot(r) for NGC 4472 (solid line) is found from Equation (1) with Pnt = 0 using the solid line approximations to the X-ray observations in Figure 2. The total mass of hot gas Mgas(r) (dot-dashed line) is relatively small. The stellar mass profile M*(r) (long dashed line) is based on a de Vaucouleurs plus core profile with mass to light ratio B = 7. The NFW dark halo profile Mnfw(r) (short dashed line) corresponds to a total mass of 4 × 1013 M. (3b Right panel:) Line of sight stellar velocity dispersion profiles (;R) as a function of projected radius R. The curves are computed from solutions r(r) of Equation (2) assuming constant which labels each curve. The observations are from Fried & Illingworth (1994).

The dark halo mass clearly dominates in Figure 3a for r R_e where M_tot(r) rises sharply above the de Vaucouleurs profile (e.g. Brighenti & Mathews 1997a; Kronawitter et al. 2000). The shape of the dark halo is consistent with an NFW halo (Navarro, Frenk & White 1996), but the virial mass of the dark halo surrounding NGC 4472 and its mass profile are poorly determined in part due to uncertainties in the hot gas temperature beyond several R_e. In addition, the X-ray image of NGC 4472 is asymmetric for r 2.5R_e, as seen in Figure 4, apparently because of its motion through the more extended Virgo cluster gas or possibly due to its interaction with the nearby dwarf irregular galaxy UGC 7636 (Irwin & Sarazin 1996; 1997). (See Fabbiano et al. 1992 for an atlas of similar figures.) In spite of these problems, the azimuthally averaged gas density profile around NGC 4472 is similar to the mean profile of about 10 other bright E galaxies out to at least 18R_e.

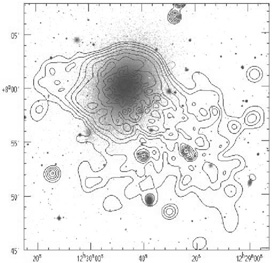Figure 4. Contours show a combined ROSAT HRI and PSPC X-ray image of NGC 4472 superimposed on an optical image from the Digital Sky Survey (Irwin & Sarazin 1996).

In non-spherical E galaxies, the existence of massive dark halos can be inferred directly from the X-ray image independent of the hot gas temperature profile - providing the gas is in hydrostatic equilibrium and rotation has little influence on the potential. For example, Buote & Canizares (1998) find that the X-ray isophotes of the E4 galaxy NGC 3923 have ellipticity _x = 0.15 ± 0.05, which is significantly less than that in the R-band, _R = 0.30. Although the gravitational potential is always more spherical than the mass distribution, Buote & Canizares show that this _x can be understood only if the confining mass is greater and more extended than any mass distribution proportional to the optical light (also: Buote et al. 2002a). Furthermore, the dark mass must have an ellipticity _dm = 0.35 - 0.66 greater than the optical image. Not only is this an elegant method to detect dark matter (see also Buote & Canizares 1996; 1997), it serves as a warning, generally ignored, that the dark matter may not be distributed in a quasi-spherical fashion.

While the hot gas in NGC 4472, NGC 4649 and NGC 720 appears to be in hydrostatic equilibrium in the stellar potential in 0.1 r / R_e 1, this circumstance may not be universal. For example, in NGC 4636 Brighenti & Mathews (1997a) found that the total mass M(r) profile found from Equation (1) (with P_nt = 0) intersects the stellar mass M_*(r) (using _B = 10.7) with no slope change whatsoever. Brighenti & Mathews argued that this insensitivity may be due to a magnetic field, B ~ 100 µG, (P_nt B² / 8) at r ~ 0.1R_e, so that the missing (P_nt / P)(d log P_nt / d log P) term in Equation (1) would account for the discrepancy. Cosmic rays or energetic turbulence would serve equally well. In fact the Chandra X-ray image of NGC 4636 shows that the hot gas is strongly agitated for r R_e (Jones et al. 2002), consistent with a breakdown in hydrostatic equilibrium. Alternatively, in reconciling the total mass M(r) of NGC 4636 from X-ray data, Loewenstein & Mushotzky (2002) reduced the contribution of the stars by lowering the stellar mass to light ratio to _B < 5.4 (at d = 17 Mpc) which is very much less than values determined for NGC 4636 from stellar velocities: _B = 10.7 (van der Marel 1991) or _B = 11.3 (Kronawitter et al. 2000) (both at d = 17 Mpc).

The shape of the stellar velocity ellipsoid (r) can also be estimated directly from X-ray observations, especially for very massive E galaxies that are approximately spherical. Here (r) = 1 - _t² / _r² depends on _r and _t = = , the velocity dispersions in the radial and transverse directions. Combining the Jeans Equation for the radial stellar velocity dispersion _r with the equation for hydrostatic equilibrium in the gas we find

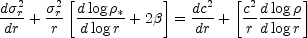(2)

where c² = kT / µ m_p is the isothermal sound speed. From Figure 2a for NGC 4472 we see that 0.5(d log _* / d log r) = d log / d log r = - 1.18 fits over -1.3 log(r / R_e) 0. The gas temperature variation is approximately linear over this region, c²(r) 4135(r_kpc + 30) (km s^-1)² (Figure 2b). If is assumed to be constant, Equation (2) can be solved analytically for _r²(r) and the line of sight stellar velocity dispersion as a function of projected radius (;R) can be found by integration (e.g. Binney & Mammon 1982). The resulting (;R), when compared with stellar velocity dispersion observations in Figure 3b, suggests = 0.530 ± 0.005, somewhat higher than that of Kronawitter et al. (2000) who use different velocity data. Conversely, if (r) is known securely from stellar data, Equation (2) can be used to determine the gas temperature profile c²(r).