2. INDUCED STAR FORMATION AND WINDS

2.1. Star Formation Processes in Interactions

Star formation induced by galaxy collisions appears similar to SF in isolated galaxies in several ways. Before merging it is often concentrated in spiral waves or bars, and tidal tails often look like extensions of the spirals. Both before and after merger it is often concentrated in nuclear starbursts. These can be orders of magnitude stronger than core bursts in isolated galaxies, but they can appear qualitatively similar.

However, there are theoretical reasons to think that the nature of collisionally induced SF is very different from that in isolated disks. In isolated star-forming disks there is evidence that SF, and gas disk structure, are self-regulated by energy and momentum feedbacks from young SF regions (e.g., Kennicutt (1989)). The self-regulation processes work to maintain a gas surface density close to the threshold for local gravitational instability throughout the disk. SF is usually concentrated in grand design or flocculent phase waves, which compress the gas, pushing its density over the stability threshold. Thus, isolated gas galaxy disks are likely examples of self-regulated, non-equilibrium steady states, at least in regions where the rotation curve is essentially flat (Note that the details of the self-regulatory processes are not well understood. See Struck & Smith (1999) for a self-consistent model in the case of strong global SF. See Zhang (2003) for a discussion of how spiral waves may be maintained for relatively long periods.)

Collisions upset steady state disks, even if they don't tear regions in them apart, as occurs in the case of direct collisions between two gas disks (e.g., Struck (1997)), or major mergers (e.g., Barnes & Hernquist (1996), Mihos & Hernquist (1996)). The waves in these disturbed disks are of a different nature than those in steady disks. For example, tidal tails are material, rather than phase waves, and in most cases induced spirals and bars have mixed material and phase aspects. Induced waves can have a very different combinations of Fourier modes than steady waves. For example, odd numbered, asymmetric modes are evidently more common.

Compressions in steady spirals can push the gas above instability thresholds and drive SF, but the degree of compression is limited by the passage time through the wave (e.g., half the epicyclic period). In material waves, compressed gas elements can move together, and maintain their compression for longer periods. Beyond this, gas clouds can be partially separated from their original surroundings, and launched like collisionless stars over substantial distances, to interact with other clouds from very different radial positions in the initial disk. This tidal mixing can sometimes involve substantial relative velocities, and may play a great role in induced SF. This point has not been studied in any detail, probably because of the difficulty in obtaining observational evidence of the mixing.

Tidal mixing is similar to collisional splash effects, where direct collisions between gas disks drive gas out of both disks, and both disks experience later fallback. Both effects are analogous to splash and mixing effects in water waves. Tidal tails are breaking waves in galaxies.

These examples highlight how detailed studies of SF in colliding galaxies can advance of understanding of SF processes in general, as well as allow us to study modes that simply don't occur in quasi-steady isolated disks. These modes are likely to be very important in the early stages of galaxy buildup. We will return to the subject of high redshift galaxies below.

2.2. Observational Samples of Star Formation Before Merger

Given these theoretical motivations, let us consider observational results. In Sec. 1 we discussed the discovery of ULIRG super-starbursts in gas-rich, major mergers in the 1980s. Generally, no such strong signal of enhanced SF has been found in pre-merger interactions. Since in most interactions there is no wholesale gas compression like that found in major merger remnants this is not surprising. The questions remain, however, do interaction induced disturbances lead to substantial SF enhancements, and if so, where, when and how? These questions were raised by Toomre & Toomre (1972) and Larson & Tinsley (1978). They have been the focus of much interest in observational studies in many wavebands of both individual systems and samples of systems (see Sec. 7 in the review of Struck (1999)).

The common conclusion was that there is an average SF enhancement in interacting systems, and that this could be result of a modest starburst in most cases. However, SF is not obviously enhanced in all interactions, and may be suppressed in some. The galaxy samples studied in the 1980s and 1990s were not generally large enough to provide strong enough statistical results to be definitive, let alone to tease out details of the relevant processes. The larger samples tended to contain systems from a wide range of pre-merger or merger stages (like the the Larson and Tinsley Arp Atlas sample), and so, could be dominated by the merger-burst effect. On the other hand, samples of specific types of interaction (e.g., the ring galaxy sample of Appleton & Struck-Marcell (1987a)) or specific stages (e.g., the Bushouse (1987) violently interacting sample) tended to be small. Interactions are rare in the present day, and specific types are therefore doubly rare!

Nonetheless, interesting clues came out of many of these studies. An important example is the Keel (1993) spectroscopic study of SF correlations in a sample of 75 Karachentsev spiral pairs (see Figure 2 for an example system). This work built on a decade of earlier work by Keel, Kennicutt and collaborators (Keel et al. (1985), Kennicutt et al. (1987)). Keel found that the current SFR (as measured by H equivalent width) did not depend much on the projected separation of the two galaxies, nor on whether a galaxy experienced the collision as prograde or retrograde. These results seem to defy the intuitive notion that strong perturbations at closest approach should drive strong responses, which could result in enhanced SF (but see Keel & Borne (2003)).

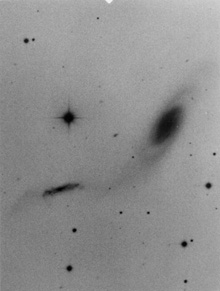Figure 2. Image of the Arp 89 system (NGC 2648, from Arp (1966). It is an example of systems studied by Keel (1993). The companion has one of the strongest nuclear SFRs in the sample.

Recently, Barton and collaborators (Barton, Geller, & Kenyon (2000), Barton Gillespie, Geller, & Kenyon (2003)) re-examined these questions with a larger sample of 502 galaxy pairs and groups drawn from Harvard redshift surveys. In contrast to Keel they found a significant anti-correlation between SF (again measured by H equivalent width) and separation of the galaxies. The two samples have comparable ranges of separation and equivalent width. Although Barton et al.'s SF-separation anticorrelation is statistically strong, it does appear to be strongly influenced by the approximately two dozen sample galaxies with equivalent widths greater than or about equal to 50. Given the relative sample size, we would expect to find only about 3-4 such systems in Keel's sample. Indeed, there are 4. Thus, it appears that the effect is too weak to have been easily detected in a sample much smaller than Barton et al.'s. Barton et al. speculate that the cause of this anticorrelation is driven gas inflow before merger in some systems.

Barton and collaborators find a second anticorrelation between SF and line of sight velocity separation between the two galaxies in each pair. This is in accord with the intuitive notion that slower passages induce stronger collisional responses. Among their pairs and groups they find a very strong anticorrelation between SF and galaxy density, which they interpret as a symptom of the well-known density-morphology relation in groups and clusters. And finally, Barton Gillespie, Geller, & Kenyon (2003) have compared their observations and models of H equivalent width and B-R broad band color, taking careful account of reddening effects. They find a significant correlation between burst population age and separation. They attribute this correlation and post-starburst spectral indicators in some systems to starburst triggering at closest approach, and subsequent aging as the galaxies move to apogalacticon.

On the other hand, Bergvall, Laurikainen, & Aalto (2003) have recently questioned the whole notion that there are statistically significant SF enhancements before merger. They examined the UBV broad band colors of a sample of 59 interacting or merging systems, and compared to a control sample of 38 isolated galaxies. They find no significantly greater scatter in the colors of Arp atlas galaxies relative to controls, in contrast to the Larson and Tinsley result, and no evidence for a significant enhancement in global SF in their interacting sample relative to the control. They do find evidence for a modest enhancement, by a factor of 2-3, in the central SF of their interacting sample. Given the previous result this implies a diminution of the average extra-nuclear disk SF in the interacting sample. Keel (1993) found no such distinction between net and nuclear SF enhancement in his sample.

On the face of it, Bergvall et al.'s primary result about the lack of SF enhancement in interactions seems to contradict many previous studies. However, these studies also find that the effect is weak if we exclude merger remnants, and the Barton et al. papers in particular suggest that we may need a sample of at least several hundred galaxies to find it. Given Bergvall et al.'s sample size, their work may not provide strong evidence for the complete absence of an effect, and they may even be a bit pessimistic in their estimate that the frequency of strong, triggered starbursts in interacting systems is of order 0.1%. Recent very large surveys of galaxy properties, like the Sloan Digital Sky Survey (SDSS) and the Two Degree Field (2dF) survey, could provide the answers, and indeed, a couple of analyses based on these surveys have been published recently.

Nikolic, Cullen, & Alexander (2004) selected nearly 12,500 pair systems with companions within 300 kpc of the primary from the SDSS. This is a volume-limited, low redshift sample with SFRs determined from SDSS (extinction and aperture corrected) H data, supplemented by IRAS data. They also reject very close pairs, i.e., most merger remnants. They find that "the mean projected star formation rate is significantly enhanced for projected separations less than 30 kpc." (see Figure 3). Like Barton et al. they find an anticorrelation between SF and the pair velocity difference. Despite its statistical significance they also found the the SF-separation anticorrelation is relatively weak, in accord with previous studies.

Figure 3. Specific star formation rates for 3 subsamples of Sloan Digital Sky Survey galaxies, selected according to absolute SFR in the ranges: 0-3, 3-10, and > 10 M yr-1 (courtesy B. Nikolic). See Nikolic, Cullen, & Alexander (2004) for details.

Lambas et al. (2003) carried out a similar pair study with 1258 pairs from the 2dF survey, and found anticorrelations of SF with separation and velocity like those in the Nikolic et al. study.

Bergvall, Laurikainen, and Aalto noted that "the interacting and in particular the merging galaxies are characterized by increased far infrared luminosities and temperatures that weakly correlate with the central activity." This result, in turn, agrees with much evidence that many specific types of interacting galaxy have enhanced far-infrared emission. For example, M51 type systems (e.g., Klimanov & Reshetnikov (2001)) on one hand, and the collisional ring galaxies Appleton & Struck-Marcell (1987a) on the other hand, both show modestly enhanced IRAS fluxes relative to the late-type disk norms.

For a broader perspective, one can turn the table and ask about the nature of galaxies with enhanced infrared emission (and usually radio continuum emission as well). We have discussed ULIRGs above, and noted that they are primarily merger remnants, and so not of interest in the present context. Luminous Infrared Galaxies (LIRGs or LIGs) and Very Luminous Infrared Galaxies (VLIRGs or VLIGs) are variously defined as galaxies with far-infrared luminosities in the approximate range 3 x 10¹⁰ - 10¹² L, and have not been studied as intensively (see examples in Figure 4). However, it appears that a large fraction of these objects are pre-merger, collisional systems with a relatively strong starburst in the core of at least one of the galaxies (see e.g., Young et al. (1996), Gao & Solomon (1999), Corbett et al. (2003), Arribas et al. (2004) and references therein). Based on statements like that of Bergvall et al. in the previous paragraph, and the rarity of LIRGs (like the ULIRGs), it seems likely that they are the same as, or more obscured relatives of, the few starburst galaxies that seem to be responsible for the weak SF enhancement found in optical pair samples.

Figure 4. Some examples of LIRG systems in B and I wavebands. Note the scale bars and the change of scale between rows. From Arribas et al. (2004), courtesy S. Arribas.

In sum, optical studies show that interactions lead to only a very small SF enhancement before merger, on average. Given that core starbursts are likely to have quite short durations (unless they have prolonged driving, e.g., Struck (2005)), it is natural to interpret this as the result of random sampling of a common process with a short duty cycle. The LIRG studies suggest another possibility, that a small minority of galaxies (the LIRGs) are responsible for the general weak enhancement, and that these galaxies are near the end of the road to merger, though not yet merged. The latter clause is supported by the fact that the few starbursts in pair samples generally have small separations and velocity separations, and this is also true for many LIRGs. In this alternative view, SF is not significantly enhanced in the early stages of interaction despite strong morphological disturbances. Also there is a more continuous increase in SF as merger is approached, an idea suggested in some of the LIRG studies. Gao and Solomon, in particular, have suggested that the phase structure of galactic ISM changes through the merger process, with an increase in the molecular phase in the final pre-merger stage (Gao & Solomon (1999), also see Gao & Solomon (2004) for similar results concerning molecular abundance changes through core starburst evolution). We will return to this discussion in Section 2.5.

2.3. Detailed Case Studies

Because it is difficult to directly translate projected galaxy separations into true separations, and directly divine the stage along the path to merging, it is difficult to use limited observations (in any waveband) to determine which of the viewpoints of the previous paragraph is correct. (Although it might be possible to estimate the separation and evolutionary stage statistically in the large samples.) There are two other ways to test evolutionary hypotheses. The first is to confront it with theory and the results of numerical simulations, which we will consider below. The second is by assembling a large library of careful case studies of specific systems. Such studies require a panchromatic array of spatially resolved and kinematic observations, which can provide strong constraints on numerical models. They also require system specific models, which closely match all available observations, and thereby provide a clear determination of the interaction stage (see discussion in Struck 2004). Given the prolonged debate on whether the nearby M51 system is the result of one or two close encounters, this is not necessarily an easy task (see review of Struck (1999)), though in either case it is clear that the system is not yet near the end of the merger road.

With a library of detailed case studies one could hope to graph SFR (or specific SFR per unit mass or gas mass) versus interaction stage to resolve the issues above. The "interaction stage" would require careful definition, however.

Detailed color and spectral synthesis modeling can in fact yield constraints, if not yet unique solutions, for the SF history of some nearby well-studied systems, e.g., the Magellanic Clouds (Zaritsky & Harris (2004), Javiel, Santiago, & Kerber (2005)), M51 (Bastian et al. (2005), Bianchi et al. (2005)), M82 (De Grijs (2001), De Grijs, O'Connell, & Gallagher (2002)) and Arp 284 Lançon et al. (2001). From such cases, one can add a few points to the hypothetical SFR-interaction stage plot.

2.4. Modes of Star Formation

Detailed case studies are also a primary tool for studying a number of specialized modes of SF, some of which have received a good deal of attention in recent years. These include: the formation of super star clusters (SSCs), SF in tidal bridges and tails, and SF in induced disk waves. Except perhaps in the last case, these modes do not usually dominate the SF in interacting systems, but they may involve physical processes unique to collisional environments, and produce especially interesting products like dwarf galaxies and halo globular clusters.

2.4.1. Tidal Dwarf Galaxy Formation

We have already mentioned early studies of SF in tidal tails in Section 1, but there has been a great of recent work. Work in this area has been energized by the possibility that, not only massive star clusters, but actual dwarf galaxies might be formed out of material in tidal tails (Figure 5). If so, this could be a means of forming dwarf galaxies at the present time, and in observable environments. In the introduction to a recent paper Duc, Bournaud, & Masset (2004) review much of the literature of the last decade, and additionally a section of the proceedings of a recent IAU symposium is also dedicated to the topic Duc, Braine, & Brinks (2004). These two sources provide a good entry points to the literature.

Figure 5. Arp atlas image (Arp 1966) of the Arp 105 system. This system contains a probable tidal dwarf galaxy at the end of the long tidal tail in the north. See Duc et al. (1997) for details.

We should begin by noting that the tidal dwarf formation has been controversial, and difficult to prove (or disprove). Most tailed galaxies do not have an obvious luminous SF region at the end of their tails. To date, only a few examples of dwarfs forming in tails have been studied in detail, so it is not clear how rare is that circumstance, nor what is the general nature of SF in tails. In fact, there are a number of difficulties in finding these objects, and confirming that they are dwarf galaxies in formation. Sometimes the tail is viewed edge-on, and if it is curved in the vicinity of the candidate dwarf a good deal of material that is not physically connected can be superposed along the line-of-sight, including multiple SF regions (e.g., Duc et al. (2000)). This can lead to large overestimates of the mass and extent of the tidal dwarf candidate, leading, in turn, to a bias for such systems in the candidate list. Determining whether a tidal dwarf candidate is truly a gravitationally bound object, and will persist as a distinct entity is also challenging, if only because of the resolution limits of observations of HI and molecular gas in these small objects.

Discussions of this latter question have been entwined with those concerning two early theories for the formation of tidal dwarfs. Barnes & Hernquist(1992) suggested that they could form as a result of gravitational instabilities in tails consisting of collisionless stars, while Elmegreen et al. (1991) argued for the dominance of gas dynamical processes in regions of enhanced turbulence (i.e., enhanced velocity dispersion). One of the difficulties in the modeling is that some density concentrations may not be persistent, and the models are not generally able to follow their evolution for very long times, or with sufficient particle resolution (but see the high resolution model of Hibbard & Barnes (2004)). Another problem in confronting these theories to observation is that since gas disks are more extensive than stellar disks, all tidal dwarf candidates are likely to contain a large fraction of gas, so it is not possible to find a case of assembly by gravitational means alone. Based on new simulations, Duc, Bournaud, & Masset (2004), and references therein] argue that only if the parent galaxy has an extensive dark halo is it likely that large amounts of gas will accumulate at the end of a tidal tail, and that this is the most efficient route to forming true tidal dwarfs with masses in excess of 10⁹ M. These authors also find that the gas accumulation process is primarily kinematic, with self-gravity playing only a minor role. It will be interesting to see how these new ideas develop in the next few years.

One of the greatest contributions of the Hubble Space Telescope to extragalactic astronomy was to resolve individual star clusters in relatively nearby galaxies and allow us to take the census the cluster populations in them. As a result of such studies it has become clear that a large fraction of new stars in colliding galaxies are formed in clusters (see Figure 6). This is difficult to quantify, but has been estimated at 50-100%. The characteristics of the most massive of these clusters, the super star clusters with estimated masses in the range 10⁵ - 10⁸ M, are just what we would expect from young clusters, so it appears that we are now able to study the formation and development of globular clusters at a variety of stages by direct observation. These studies have given rise to a considerable literature, which extends far beyond the topic of this review, so we only describe a few of the relevant highlights.

Figure 6. HST image of young star clusters in the merging Antennae galaxies, from Whitmore et al. (1999), courtesy of B. Whitmore].

In a summary of a recent conference on this topic, O'Connell (2004) emphasized the universality of the properties of young cluster populations, despite a huge range of formation environments and scales. These properties include a nearly universal power law mass function, which evolves naturally with time to the exponential function of old globulars. The number of clusters and the maximum cluster luminosity in a star-forming region both scale with total SFR. Most cluster populations have a very small range of formation ages. This is especially true of populations in galactic nuclei, but in colliding galaxies with widely spread SF regions there can be distinct populations, each with small age spreads (e.g., Alonso-Herrero et al. (2002)). The spatial structure of super star clusters also appears to be universal. The stellar initial mass function is universal, at least at the high end where it can be determined.

It is worth emphasizing the range of environments where super star clusters and their somewhat less massive relatives are found in colliding galaxies. Of course, starburst nuclei are primary locations and M82 (De Grijs (2001), Melo (2005)) is probably the most famous example. M51 (Bik et al.(2003), Bastian et al.(2005)) is also very interesting. At the other extreme we have globular cluster populations of intermediate age (i.e., of order a few Gyr) around merger remnants. In the ongoing merger in the Antennae system, clusters are scattered at many locations in the bodies of the galaxies Whitmore & Schweizer (1995). Massive young clusters are found in many tidal tails, though interestingly Knierman et al. (2003) make a suggestion, based on their study of 6 tail regions, that they either have a population of massive young clusters or a tidal dwarf, but not both. This conjecture certainly merits further observational and modeling study. Massive cluster populations are also found in ring galaxies like the Cartwheel Appleton et al. (1996) and ocular waves like IC 2163 Elmegreen et al. (2000). It seems very likely that the mid-infrared detectors on the Spitzer Space Telescope will find massive cluster populations in more environments that are hidden from Hubble and ground-based telescopes.

What do these environments have in common and what's the physics behind massive cluster formation? O'Connell (2004) summarizes the prevailing view that the formation of SSCs requires high gas pressures, of order 10⁴ times those of the interstellar medium in the solar neighborhood, and that these high pressures must extend through a region of size greater than 1 kpc (also see Schweizer (1998)). Strong turbulence also pervades the formation region. O'Connell emphasize that the energetic environment inside a forming massive cluster must be truly extraordinary.

It is likely that all of the colliding galaxy environments noted above are able to achieve the high pressures and turbulence that the theory says are necessary to form the super star clusters. This is not entirely clear in the case of disk waves and tidal tails. However, in the former case the process may be aided by feedback effects from the first stars to form. In the case of tails it may simply be that some achieve the requisite conditions and form massive clusters, and others do not. We have much to learn yet about these processes.

Finally, O'Connell notes a couple examples of nuclear starbursts where the super star clusters are much more massive than the other clusters, and so, the mass function is discontinuous. He speculates there may be a special formation mode for these cases, though the nature of that mode is not clear. As in the case of tidal dwarf formation there are competing mechanisms, and one of these may dominate only in the exceptional cases. These mechanisms again include the formation of massive progenitor clouds triggered directly via gravitational instability, or indirectly in dense environments assembled by large scale gravitational instability. They may also include hydrodynamic effects like cloud crushing that occurs when giant clouds experience an abrupt pressure increase after impacting large-scale shocks or other high pressure regions (Jog & Solomon (1992), Braine et al. (2004), Bekki et al. (2004)). The combination of these processes could probably generate discontinuous cluster mass functions, but at present, this is only speculation.

A few more exotic ideas have also been discussed recently. Scannapieco, Weisheit, & Harlow (2004) have suggested that strong winds from young galaxies could have shocked their dwarf companions, stripping gas and compressing it to form globular clusters. Burstein et al. (2004) also suggest that globulars might form in dwarf companions. Their argument is based on a hierarchical clustering model of galaxy formation as applied to the cluster populations in the Milky Way and M31. On the other hand, Hibbard, Vacca, & Yun (2000) have found several examples of systems where winds seem to have swept the gas out of parts of tidal tails, without the production of massive star clusters.

2.4.3. ULXs

Ultraluminous X-ray sources (ULXs) are defined as having X-ray luminosities of order 10³⁹ - 10⁴¹ ergs per s^-1, which extends beyond the luminosities of the well-studied high mass X-ray binaries, but is still much less than a typical active galactic nucleus. X-ray sources of this luminosity have been detected in galactic nuclei for two decades, but the arcsecond resolution of the Chandra Observatory has facilitated their discovery and definition as a class of objects (see reviews of Mushotsky (2004a), van der Marel (2004), Ward (2003)).

Estimates indicate that they may be a quite common constituent of the nuclei of normal galaxies. However, their nature remains somewhat mysterious. There are two leading theories. The first is that they are indeed an extension of the high mass ( 10 M) binary phenomenon, but with highly super-Eddington accretion rates and beamed emission (e.g., Begelman (2002), King (2004), King & Dehnen (2005), Liu, Bregman, & Irwin (2005)). The second is that these are in fact black hole accretion systems of intermediate mass between stellar black holes and active nuclei, e.g., masses > > 100 M (e.g., Hopman et al. (2004), Krolik (2004), Miller, Fabian, & Miller (2004), Miller (2005)). There are strong arguments for both models. For the most luminous ULXs the stellar mass explanation is strained. For the most rapidly variable ones the source size and mass is limited from above. Since the luminosity bounds of the class are ad hoc, it is certainly possible that the class includes both kinds of source. Gutiérrez & López (2005) also present a cautionary tale of how apparent ultraluminous sources can in fact be background sources.

A number of galaxies are now known to contain enough ULXs to allow the construction of luminosity functions, and these luminosity functions are found to scale with total SFR or a combination of SFR and galaxy mass (e.g., Swartz et al. (2004)). Over the last 5 years ULX populations have been found in several colliding galaxies, including M82 (Fiorito & Titarchuk (2004), Matsumoto et al. (2004), Portegies Zwart, Dewi, & Maccarone(2004) and references therein), the Antennae, the Cartwheel ring galaxy, and the ring-tailed Arp 284 system (Figure 7). The ULXs are widely spread across the Antennae (Fabbiano et al. (2004), Miller et al. (2004). They are found in the outer ring and an X-ray bridge of the Cartwheel (Gao et al. (2003), Wolter & Trinchieri (2004)). In Arp 284, most are associated with tidal features, especially a prominent tail, but with one of the brightest known contained in the ring (Smith, Struck, & Nowak (2005)). Some of these ULXs are associated with star-forming regions, and so they provide another locator and probe of such regions that is not easily obscured.

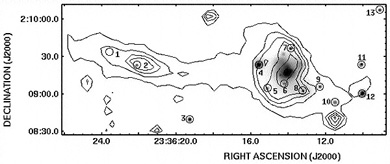Figure 7. Smoothed greyscale X-ray image of the Arp 284 system from Chandra Observatory data, with luminous point sources numbered. Contours showing the optical outline are derived from the Digital Sky Survey image. See Smith, Struck, & Nowak (2005) for details.

2.5. Summary and Theory

Clearly, there has been a vast amount of work on interaction induced SF in the last few decades, and we have only been able to skim through it above. Is all of this work leading to a comprehensive understanding of the phenomenon? Perhaps not quite yet, but we may be getting close to that goal. The question can be broken down into several separate questions. First of all, do we understand the general physical processes, and do we understand enough about how they work to account for the general observational systematics? Secondly, do we understand these processes well enough to reproduce their effects in numerical models, both comprehensive models of specific systems, and models of SF in particular dynamical processes?

2.5.1. Numerical Models

We'll begin by considering recent numerical models and some aspects of the last question. Star and star cluster formation take place on scales that are orders of magnitude smaller than those typically resolved in simulations of galaxy collisions. However, separate models of the process on those small scales are beginning to advance our understanding greatly. Because of this, and the fact that much of the dynamics on the intermediate scales is essentially scale-free turbulence, we may be able to develop reasonably accurate SF formulations, without needing to resolve the scales on which it occurs. However, to date, relatively simple SF prescriptions have been used in galaxy collision models. Moreover, these prescriptions have been based on several different ideas about the dominant SF triggering process. Three of the most popular are: 1) a simple density-dependent SFR, 2) triggering by strong compressions in cloud-cloud collisions or large-scale shock waves, or 3) triggering by gravitational instability above a threshold density (or surface density or pressure).

With regard to the first of these, the Schmidt Law, in which the SFR is proportional to a low power of the gas density, surface density, or the gas density divided by a local dynamical time has been surprising resilient. Mihos, Bothun, & Richstone (1993) used it (and isothermal particle hydrodynamics) to model collisions between two disk galaxies, and Mihos & Hernquist (1994) used it to model the Cartwheel ring galaxy. In both cases they found that the models gave about the "relative intensity and morphology of induced star formation." Later, Mihos & Hernquist (1996) found that with this formulation mergers between disk galaxies with bulges could produce burst SFRs a hundred times larger than those of isolated galaxies. They also explored how the presence of a bulge component affected the merger SFR. Given the simplicity of the prescription the results are impressive. However, Cox et al. (2005) have recently shown that the amount of SF in mergers may have been overestimated in earlier models, because this quantity depends on how conservation conditions are implemented in the SPH algorithm.

Phenomenological cloud collision models for gaseous dissipation in galaxies go back to the 1970s. The obvious disadvantage of such models is that interstellar gas clouds are transient, ever-changing structures, and not the coherent entities implicitly assumed when equating them with the 'sticky' (i.e., dissipative) particles of a numerical model. On the other hand, it is a straightforward way to model the cloud collisions and shock encounters which occur in many types of collision. In models of polar ring galaxies Bekki (1997), models of starbursts in multiple mergers Bekki (2001), and in other applications, Bekki has used a hybrid particle model. In his models there is dissipation from cloud collisions, but a probabilistic Schmidt Law is used to convert selected gas particles to stars. The local gas density is computed for each gas particle and used in the Schmidt Law.

Recently, Barnes (2004) has proposed a rather sophisticated phenomenological model, in which SF depends on the amount of energy dissipation in shocks. He argues that with this prescription he is able to produce a much better model of the Mice system (NGC 4676) than with a Schmidt Law. This is one of the few significant comparisons of different formulations in models of the same system. Barnes also notes that Schmidt Law models are quite insensitive to details of the interaction, while shock induced SF is very sensitive, and could be checked observationally.

Threshold instability models have been used frequently in the areas of galaxy formation and multiphase models of galaxy disks in recent years. This author has used such a model with feedback and gas with a continuous range of thermal phases in studies of direct collisions between two gas disks and their reformation Struck (1997). More recent work on disk collisions with many more particles has been carried out by Springel & Hernquist (2005). Cox et al. (2005) have recently presented an efficient effective equation of state approach to handling the thermal physics.

I have also used this type of SF formulation in detailed N-body hydrodynamic models of a couple of specific systems with extensive observational data (Struck & Smith (2003), Struck (2005)). Both the spatial distribution of SF and the history of net SF fit the observational constraints, though the constraints on the SF history are not stringent. At low threshold densities this type of formulation is probably much like the Schmidt Law, since the SF will occur in regions with the most particles (i.e., high density). With a high threshold density, a violent process like shock compression and subsequent cooling will be needed in many cases to drive SF, more like the Barnes model.

In the end we see that many different numerical treatments can simulate induced SF reasonably well, and so none are immediately falsifiable. The answer to the question posed at the beginning of this discussion is yes, we can reproduce observations, but not because the models represent the underlying physical processes especially faithfully. The universality of those processes, and their highly interconnected properties, allow modelers to use simple formulations on large scales. Stringent tests of feedback prescriptions may eventually come by fitting the mass fraction and distribution of warm-to-hot phases in the interstellar gas. However, this will take much more realistic modeling of the thermal physics, and the stellar initial mass function, than is currently the norm.

Detailed observational studies on kiloparsec scales in various environments may provide insight into how sensitive SF is to compression and dynamical timescales. Spitzer Space Telescope observations in the mid-infrared have the ability to see through obscuring dust and provide a complete SF census on these scales in nearby galaxies, so the prospects are exciting in the next few years.

2.5.2. Squeezing Out Stars

All of the models described above, form stars by compressing gas (albeit in more or less finely tuned ways). This recalls the Kennicutt (1989) observational result on the universality of the Schmidt Law over a range from isolated galaxies with modest SFRs to ULIRGs. Apparently, the first law of induced SF is - it's just the (large-scale) compression. More precisely, it appears that large-scale compression drives a turbulent cascade, which enhances star-forming compressions on the small scales (e.g., Krumholz & McKee (2005), and references therein). Because of the universality of the cascade, this process doesn't necessarily depend much on the details at the large and small scales.

In the case of ULIRGs the spectacular response is the result of spectacular angular momentum transport and compression in the major merger. For rapid or distant encounters the most that can be achieved are relatively small compressions in bars and waves. It is worth recalling that basic tidal forces stretch along the line of galaxy centers and compress in the perpendicular directions. For an approximately two-dimensional disk this means (very roughly!) stretching in one dimension and compressing in one dimension. Alternately, in terms of a simple impulsive torque, it means that angular momentum is added to one side of the disk (stars are pulled ahead in their orbits), and subtracted from the other side (stars are pulled back). Thus, net compression across the disk is roughly balanced by stretching or torque-induced rarefaction. In either case, the global effects are modest for small amplitude disturbances, implying little induced SF, as observed in such cases. On the other hand, in strong disturbances, the torque-induced decelerations of the gas orbital motion, and subsequent compression of a significant fraction of the gas, may be enough to induce a strong starburst, regardless of the fate of the rest of the gas.

LIRGs seem to be a heterogeneous class, but they include interacting galaxies that are separated by about 1-2 diameters of the larger. In such cases the tidal effects are nonlinear. In addition, the gravitational forces within each disk will be augmented by dark matter from the other galaxy's halo, which is coextensive with the disk. (In fact, the importance of this effect must be estimated quantitatively, but generally it will become important at the separations cited.) The resulting global compressions can account for the SF enhancement. It appears that such cases play an important part in creating the observed anti-correlation between SFR and the separation of the two galaxies.

In sum, it appears that the general systematics of induced SF can indeed be accounted for, to first order, as the direct result of compression. The consequence of this, that we can learn little more about SF physics from large scale studies, is disappointing. On the other hand, it means that colliding galaxy model results are not sensitive to many details of the SF/feedback formulation, and that there is little point in trying to extend numerical resolutions to very small scales. (However, we will eventually have much higher observational and modeling resolutions, which would allow the study of the cloud turbulent cascade, and the full effects of the non-equilibrium interaction environment. The point is that modest resolution improvements will not help much.)

We conclude with a brief mention of some possible exceptions or refinements to the "it's just compression" rule. The first might be found in the environment of core starbursts. If these are triggered by strong shocks, or with a sensitive threshold, then they may turn on rapidly. If, instead, they obey the Schmidt Law they will turn on more slowly if the central gas mass and density accumulate slowly. Generally, current spectral synthesis techniques are not able to provide SF histories that are accurate enough to distinguish. That is, except in a few nearby starburst cores, where the evidence seems to favor rapid turn-on of local density concentrations (because of the small age spreads within these concentrations, e.g., Harris et al. (2004)). Similarly, the study of core burst turnoff might be enlightening. There seem to be regions in the core of M82 where the cloud system is disrupted, SF is turned off, but pressures and gas densities remain high (Mao et al. (2000) and references therein). The existence of such regions may necessitate at least a caveat in the Schmidt formulation.

We might be able to derive more information by studying SF within and behind density waves in disks. Spiral waves are ubiquitous, but ring waves produced in direct galaxy collisions are simpler. Asymmetric rings produced in slightly off-center collisions are the most interesting because they are still simple, but the wave amplitude varies continuously with azimuth. This is an excellent environment for confronting threshold versus continuous theories, at least if the compression in part, but not all, of the ring exceeds the threshold. To date, there is some evidence in support of thresholds, but not without complications ranging from incompletely known obscuration to unknown details of the collision parameters. The primary example is the Cartwheel ring with large variations of SFR and cluster populations around the ring, but with uncertainty about the details of the collision, and no old star component in the ring to provide independent information about wave amplitude as a function of azimuth (Appleton & Struck-Marcell (1996)). With its relatively high resolution and ability to see through much obscuration, the Spitzer space telescope could resolve these ambiguities in carefully chosen systems.

There are many more examples of how to get beyond the simple compression law and the first-order theory of induced SF, and such work should become increasingly important in this field.